Investigate each of the following for .

Describe each when a=b, a<b, and a>b.

, ,

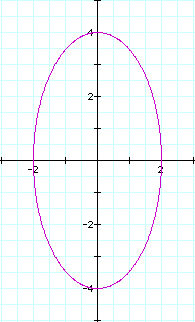
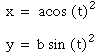Consider

If a=b, this parametric equation show a circle with a radius=abs(a). To explore Click here

 

Why does the equation become a circle?

We know that and is a equation of a circle with radius r.

Since

,

we can get a equation

i.e. .

 

 

If a>b, this parametric equation show a ellipse like the follwing figure(a=6, b=1)

To explore Click here

 

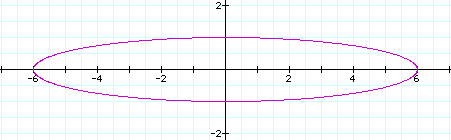
If a<b, this parametric equation show a ellipse like the follwing figure(a=2, b=4)

To explore Click here

 

Why does these equations become ellipses?

We know that and is a equation of an ellipse passing through (a,0), (-a,0), (0,b), (-b,0).

Since

,

we can get a equation

i.e the equation of a ellaipse.

 

 

Consider

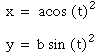
If a=b, this parametric equation show a line y=-(x-a)+a in any one quadrant. To explore Click here

If a>b or a<b, this parametric equation show a line y=-(x-a)+b in one quadrant determined by tha values of a and b.

The following is a graph when a=5, b=2.

To explore when a>=2 and b=2 Click here

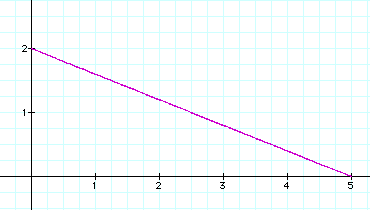
This is a graph when a=2, b=5.

To explore in a case of a=2 and b>=2 Click here

 

Why does these equations become lines?

Since

and ,

we can get a line equation .

This eqation says that x-intercept is a and y-intercept is b.

 

 

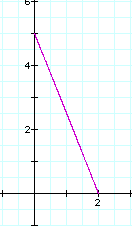
Consider

If a=b then the graph is like the following(a=b=3 or a=b=-3)

 

To explore Click here

 

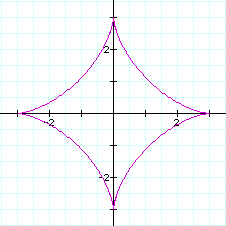
If a>b then the graph is like the following(a=5 or -5, b=2 or -2 )

To explore Click here

 

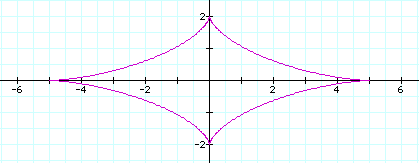
If a<b then the graph is like the following(a=2 or -2, b=5 or -5)

To explore Click here

 

Let's graw the figures above simultaneously.

 

My Conjecture

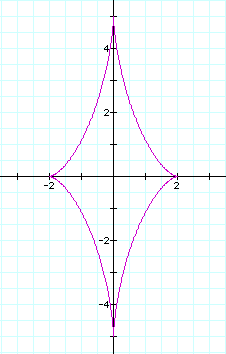
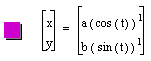
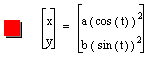
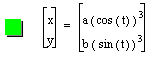
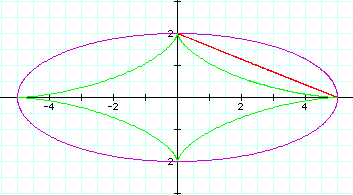
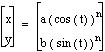is a curve shape gradually approaching to axises as n is increasing.

If n is odd then the graph appears all quadrants and if even then is does one quadrant dependinng on the values of a and b.

We can investigate this cojecture by click here.

Return to Hyungsook's homepage