Untitled Document

Interpret your graphs.

What happens to

(i.e., the case where b=1 and c=2) as a is varied? Is there a common point to all graphs? What is it? What is the significance of the graph where a = 0? Do similar interpretations for other sets of
graphs. How does the shape change? How does the position change?

Let's see the graph of

when a=-2, -1.5, ..., 1.5, 2.

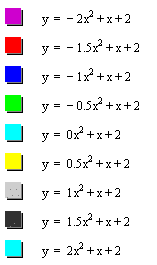
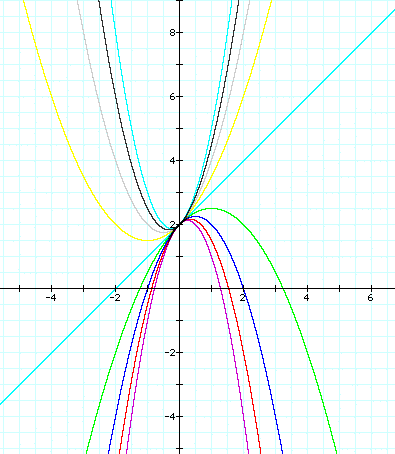
We can see that as a is varied, the width and vertex of is varied but

all graph pass through (0,2).

How do the graphs varied?

Case 1) a>0

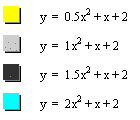
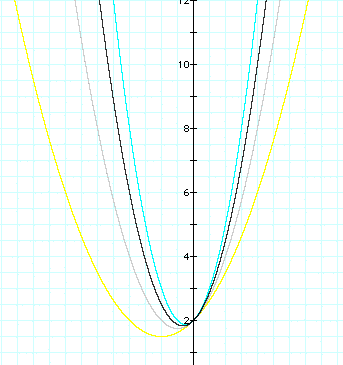
We can know that the width of the graph is gradually wider as a is close to zero and the verttices are on the left hand side of the y-axis

Case 2) a = 0

Our equation becomes a line

i.e

Case 3) a<0

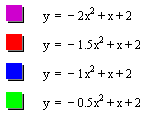
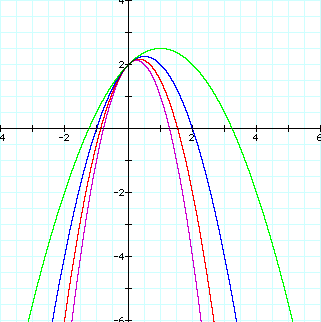
Likewise a>0, we can know that the width of the graph is gradually wider as a is close to zero and the verttices are on the right hand side of the y-axis

Our Result

1) As the value of a is close to zero, the width of the grapgh becomes wider

(i.e. as the absolut value of a is decreasing, the width of the grapgh becomes wider)

2) As the value of a is decreasing, the vertex moves towards left-down passing through (0,2)

3) All graph of the equation above pass through (0,2)

4) If a>0 then the grapgh is concave and if a<0 then the graph is convex

Further Study

How do the vertices of the graphs vary?

First, let's consider carefully the trace of the vertex of

Explore the trace

We can infer that a trace of the vertices becomes a line passing through (0,2)

Second, let's consider carefully the trace of the vertex of