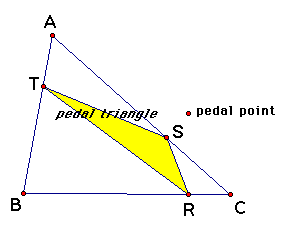
The investigation of the Pedal Triangle
associated with a Pedal Point of a triangle
What is a Pedal Triangle?
If P is any point in the plane, then the triangle formed
by constructing perpendiculars to the sides of ABC locate three
points R, S, and T that are the intersections. Triangle RST is
the Pedal Triangle for Pedal Point P.
 To investigate the pedal triangle for any pedal point
CLICK HERE
To investigate the pedal triangle for any pedal point
CLICK HERE
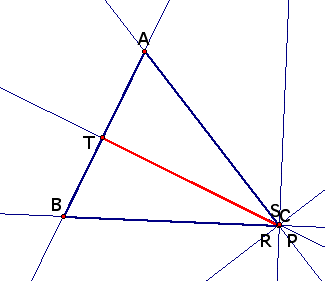
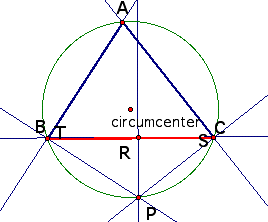
We can notice there is some instances that Pedal triangle is
degenerated. Of course, if P is a vertex then Pedal triangle becomes
a height of the triangle through the vertex.
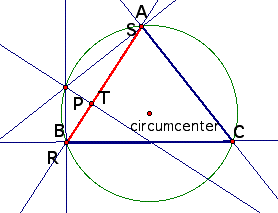
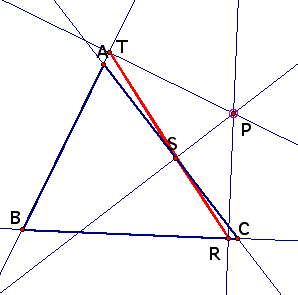 Conditions in which
the three vertices of the Pedal triangle are colinear
(This line segment
is called the Simson Line)
Conditions in which
the three vertices of the Pedal triangle are colinear
(This line segment
is called the Simson Line)
Through an exploararion we can know that if P is inside traiangle
then Pedal triangle is always made. And then where
of outside is a Pedal triangle degenerated?
Construct a circle with circumcenter
of ABC as center and with larger radius than cicumcicle radius.
And then observe the Pedal triangle. Let's see the locus of the
midpoints of the sides of the Pedal triangle as P is animated
around the circle.
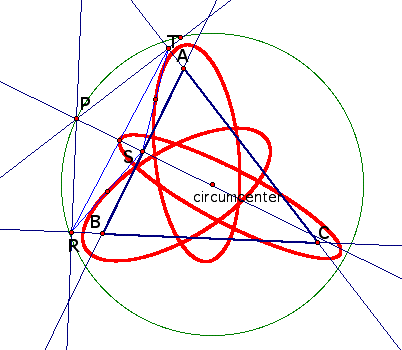 Three locuses are ellipses.
What if the circle is circumcircle?
We can explore that Pedal triangle is degenerated if a pedal point
is on circumcircle. Click here.
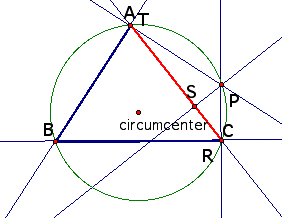
Is there a point on the circumcircle
for P that has side AC as its Simson line? AB? BC? Yes.
Three locuses are ellipses.
What if the circle is circumcircle?
We can explore that Pedal triangle is degenerated if a pedal point
is on circumcircle. Click here.
Is there a point on the circumcircle
for P that has side AC as its Simson line? AB? BC? Yes.
 What is the relationship
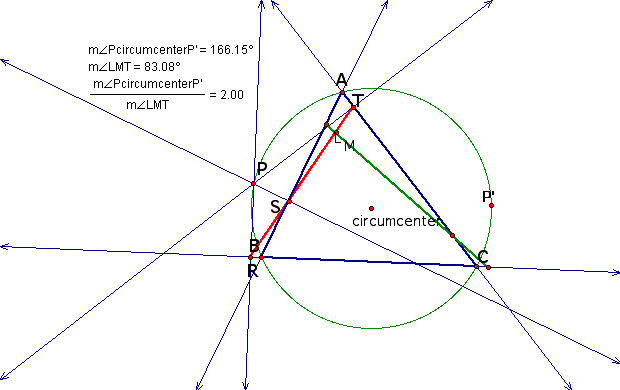
between two Pedal points and their Simson lines?
Through exploartion(Click here)
by GSP, there is relationship of twice
angle between the angle made by pedal points and circumcenter
and the one made by two Simson lines.
What is the relationship
between two Pedal points and their Simson lines?
Through exploartion(Click here)
by GSP, there is relationship of twice
angle between the angle made by pedal points and circumcenter
and the one made by two Simson lines.
Return to
Hyungsook's homepage








