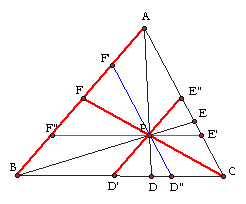
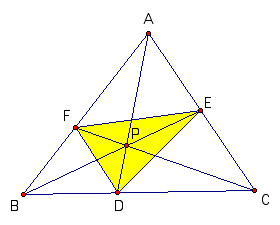
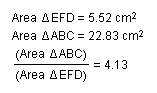A. Consider any triangle ABC. Select a point P inside
the triangle and draw lines AP, BP, and CP extended to their intersections
with the opposite sides in points D, E, and F respectively.
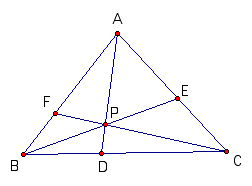
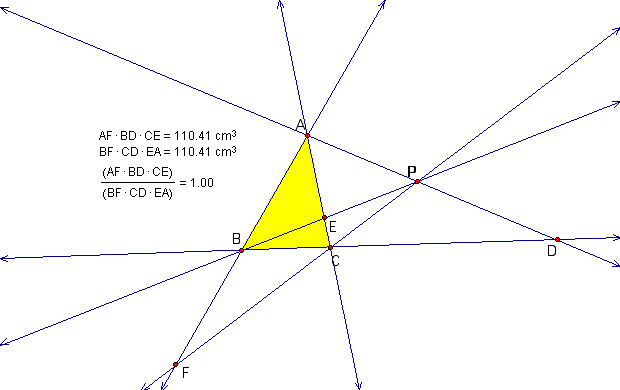
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles
and various locations of P.
B. Conjecture? Prove it! (you may need draw some
parallel lines to produce some similar triangles) Also, it probably
helps to consider the ratio
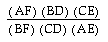
Can the result be generalized (using lines rather than segments
to construct ABC) so that point P can be outside the triangle?
Show a working GSP sketch.
C. Show that when P is inside triangle ABC, the ratio
of the areas of triangle ABC and triangle DEF is always greater
than or equal to 4. When is it equal to 4?
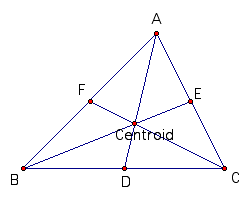
A. If P is centroid then we can
know (AF)(BD)(CE) = (FB)(DC)(EA)
since AF=FB, BD=DC, and CE=EA.
If ABC is isosceles triangle and P is orthocenter then FBC
is congruent to ECB and B is midpoint.
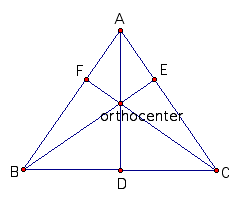
So AF=AE, FB=EC, and BD=DC. Therefore
(AF)(BD)(CE) = (FB)(DC)(EA).
To explore this relationship for various triangles and various
locations of P through GSP, Click here.
We can see that (AF)(BD)(CE) is always same to (FB)(DC)(EA).
B.Conjecture
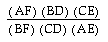 is equal to 1
is equal to 1
Proof)
Let's draw segments parallel to each side and passing through
P.
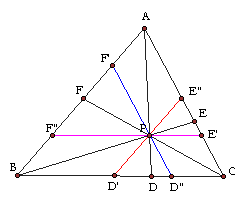
i.e F"E is parallel to BC, D"F' is parallel to CA,
and E"D' is parallel to AB.
I will prove as showing that AF, FB, BD, DC, CE, EA can be
expressed by AD, BE, CF, PA, PB, PC, PD, PE, PF using similar
triangles.
Since ABD is similar to PD'D and ACD is simailr to
PD"D,
AD:PD = AB:PD' = AC:PD"
--- (1)
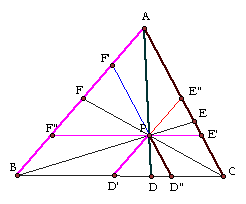 Since BCE is similar to PE'E and BAE is similar to
PE"E,
BE:PE = BC:PE' = AB:PE"
--- (2)
Since BCE is similar to PE'E and BAE is similar to
PE"E,
BE:PE = BC:PE' = AB:PE"
--- (2)
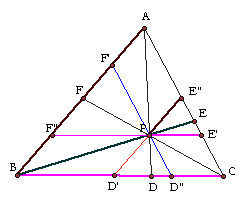 Since CAF is similar to PF'F and CBF is similar to
PF"F,
CF:PF = CA:CF' = CB:PF"
--- (3)
Since CAF is similar to PF'F and CBF is similar to
PF"F,
CF:PF = CA:CF' = CB:PF"
--- (3)
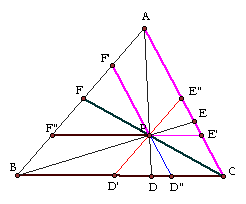 Since F"E' is parallel to BC, AF"P is similar
to ABD and AE'P is similar to ACD. Thus
AP:AD = F"P:BD = PE': DC
--- (4)
Since F"E' is parallel to BC, AF"P is similar
to ABD and AE'P is similar to ACD. Thus
AP:AD = F"P:BD = PE': DC
--- (4)
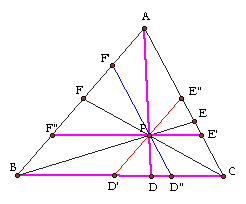 Since D"F' is paralle to CA, BD"P is similar
to BCE and BF'P is similar to BAE. Thus
BP: BE = D"P:CE = PF':EA
--- (5)
Since D"F' is paralle to CA, BD"P is similar
to BCE and BF'P is similar to BAE. Thus
BP: BE = D"P:CE = PF':EA
--- (5)
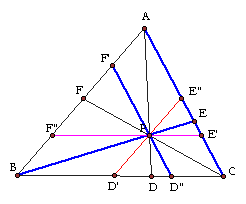 Since E"D' is parallel to AB, CE"P is similar
to CAF and CD'P is similar to CBF. Thus
CP:CF = E"P:AF = PD':FB
--- (6)
Since E"D' is parallel to AB, CE"P is similar
to CAF and CD'P is similar to CBF. Thus
CP:CF = E"P:AF = PD':FB
--- (6)
 By (6), AF = CF/CP*E"P
= (CF/CP)*(PE/BE)*AB since (2)
FB = CF/CP*PD' = (CF/CP)*(PD/AD)*AB
since (1)
By (5), CE = BE/BP*D"P
= (BE/BP)*(PD/AD)*AC since (1)
EA = BE/BP*PF' = (BE/BP)*(PF/CF)*CA since (3)
By (4), BD = AD/AP*F"P
= (AD/AP)*(PF/CF)*CB since (3)
DC = AD/AP*PE' = (AD/AP)*(PE/BE)*BC since (2)
By (6), AF = CF/CP*E"P
= (CF/CP)*(PE/BE)*AB since (2)
FB = CF/CP*PD' = (CF/CP)*(PD/AD)*AB
since (1)
By (5), CE = BE/BP*D"P
= (BE/BP)*(PD/AD)*AC since (1)
EA = BE/BP*PF' = (BE/BP)*(PF/CF)*CA since (3)
By (4), BD = AD/AP*F"P
= (AD/AP)*(PF/CF)*CB since (3)
DC = AD/AP*PE' = (AD/AP)*(PE/BE)*BC since (2)
Let's calculate AF/FB, BD/DC, and CE/EA.
AF/FB = (PE*AD)/(PD*BE)
BD/DC = (PF*BE)/(PE*CF)
CE/EA = (PD*CF)/(PF*AD)
Therefore,
(AF/FB)(BD/DC)(CE/EA) = (PE*AD*PF*BE*PD*CF)/(PD*BE*PE*CF*PF*AD) = 1
----- End of proof -----
Can the result be generalized
so that point P can be outside the triangle?
We can generalize this fact even though P is outside the triangle.
To explore Click here.
C.The
ratio of the area of two triangles
We can see that the ratio of the areas of ABC and DEF is always
greater than or equal to 4. To explore Click
here.
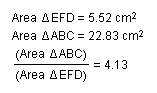
Conjecture:
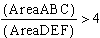 or euqal to 4
or euqal to 4
Proof)
At first, I will show that triangle PDE,
PEF, PFD can be expressed triangle ABC.
PDE = BDE * (PE/BE) = BCE * (BD/BC)
* (PE/BE) = ABC * (CE/AC) * (BD/BC) * (PE/BE)
PEF = CEF * (PF/CF) = AFC * (CE/AC)
* (PF/CF) = ABC * (AF/AB) * (CE/AC) * (PF/CF)
PFD = AFD * (PD/AD) = ABD * (AF/AB)
* (PD/AD) = ABC * (BD/BC) * (AF/AB) * (PD/AD)
Since DEF = PDE + PEF + PFD,
DEF = ABC * (CE/AC) * (BD/BC)
* (PE/BE) + ABC * (AF/AB) * (CE/AC) * (PF/CF) + ABC * (BD/BC)
* (AF/AB) * (PD/AD).
I. e. DEF = ABC * ( (CE/AC) *
(BD/BC) * (PE/BE) + (AF/AB) * (CE/AC) * (PF/CF) + (BD/BC) * (AF/AB)
* (PD/AD))
Therefore,
DEF/ABC = (CE/AC) * (BD/BC) *
(PE/BE)
+ (AF/AB) * (CE/AC) * (PF/CF) + (BD/BC) * (AF/AB) * (PD/AD) --- (*)
We know that
AF = (CF/CP)*(PE/BE)*AB
FB = (CF/CP)*(PD/AD)*AB
Since AB = AF + FB and AB = CF/CP*(PE/BE + PD/AD)*AB,
CF/CP*(PE/BE + PD/AD) = 1
PE/BE + PD/AD = CP/CF = (CF -
PF)/CF = 1 - PF/CF
PF/CF + PE/BE + PD/AD = 1
Let AF/AB = a, BD/BC = b, CE/CA = c,
PE/BE = x, PF/CF = y, PD/AD = z. Then (*) can be expressed by
DEF/ABC = bcx + acy + baz and x + y + z = 1
I will show that a,b, and c can be expressed
by x, y, and z.
Since AF/FB = (PE/BE)/(PD/AD) = x/ z,
FB = AB - AF, and a/(1 - a) = x / z,
a = x / (x + z ) and a = x /
(1 - y )
Simiary, b = y / (1 - z ) and
c = z / (1 - x )
ABC/DEF = xyz/((1-z)(1-x)) +
xyz/((1-x)(1-y)) + xyz/((1-y)(1-z)) = xyz(1-y + 1-z + 1-x)/((1-x)(1-y)(1-z))
= 2xyz/((1-x)(1-y)(1-z))
DEF/ABC = 2xyz/(xy + yz +
xy - xyz)
We know that
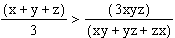 or
equal when x=y=z(The relation of Arithmetic mean and Harmonic
mean)
or
equal when x=y=z(The relation of Arithmetic mean and Harmonic
mean)
Since x + y + z = 1 and xy + yz + zx >= 9xyz,
DEF/ABC <= 2xyz/(9xyz-xyz)
DEF/ABC <= 1/4
Thus ABC/DEF>=
4
Also we know that ABC/DEF=4 when x=y=z=1/3. Therefore
P has to be a centroid
for the ratio to be 4
----- End of proof -----
We can notice easily that if P is a centroid then DEF
= ABC/4.
Since D, E, and F are midpoints, DEF is similar to
ABC with the ratio 1/2.
Therefore the area of DEF is a quarter of ABC
Return to
Hyungsook's homepage