Assignment 10

Parametric Equations

By Carly Coffman

A parametric curve in the plane is a pair of functions

x = f(t)

y = g(t)

 

where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent
of the curve will depend on the range of t and your work with parametric equations should pay close attention the range of t . In many applications,
we think of x and y "varying with time t " or the angle of rotation that some line makes from an initial location.

Various graphing technology, such as the TI-81, TI-82, TI-83, TI-85, TI-86, TI-89, TI- 92, Ohio State Grapher, xFunction, Theorist, Graphing
Calculator 2.1, and Derive, can be readily used with parametric equations. Try Graphing Calculator 3.1 or xFunction for what is probably
the friendliest software.

First Exploration

x = cos (t)

y = sin (t)

for t greater than or equal to 0 and less than or equal to 2 pie

 

Let's take a look at the graph.

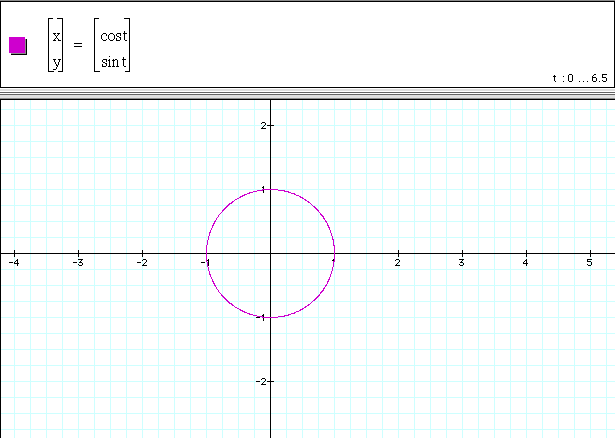
We see that the graph is a circle with radius one. Let's look at some of the defined pairs. If we start with t=0, then cos (0)=1 and sin(0)=0. Thus, the point (1,0) is graphed. Then, if we look at , then and . So, the point (0,1) is graphed. If you graph every point for t greater than or equal to 0 and less than or equal to 2 pie, you get the continuous function, .

Second Exploration

x = cos (at)

y = sin (bt)

for t greater than or equal to 0 and less than or equal to 2 pie

 

Notice that there are three different cases we can study here, a=b, a<b, and a>b.

Case 1: a=b

Let us first graph a=b=100 and a=b=1.

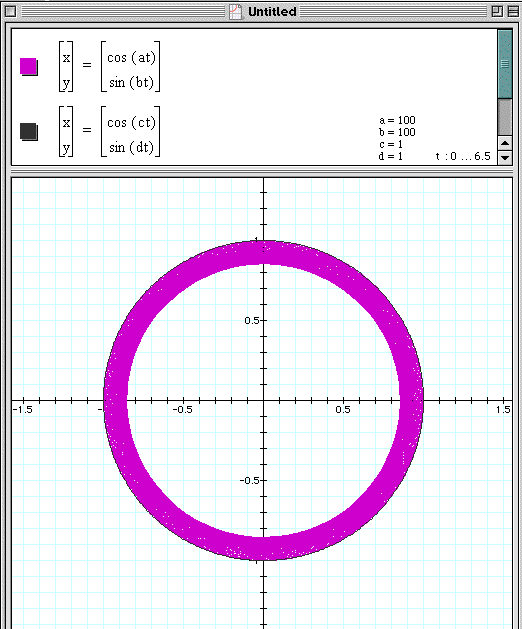
Using graphing calculator, we see that as a and b increase the thickness of increases as well.

Let's also look at a negative value and a=b=0.

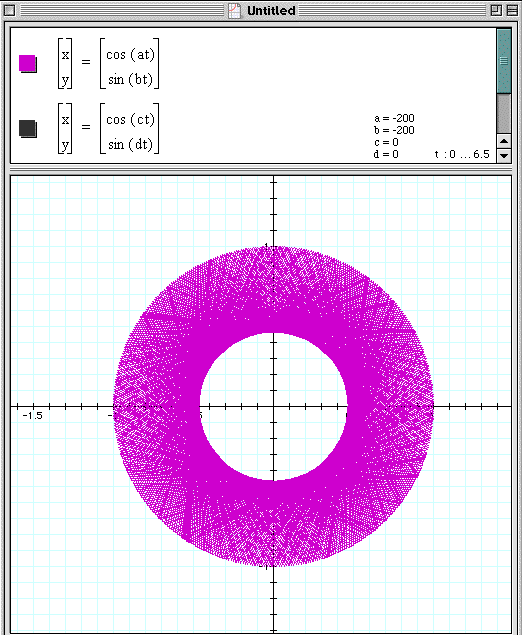
When a=b=0, there is no continuous function. Take a look at what happens when a=b=-200 though! The thickness increased like it did with large positive values of a and b. When studying these trends, it seems that there is either a limit of thickness for the graph or that if a and b are large enough, the graph will fill in the area of the circle, .

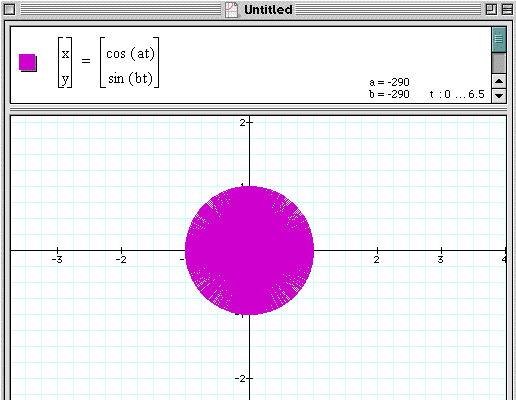
When a=b=-300, the function seems to fill in the area of the circle . However, when zooming in we find that the circle area is not complete, which is shown below.

 

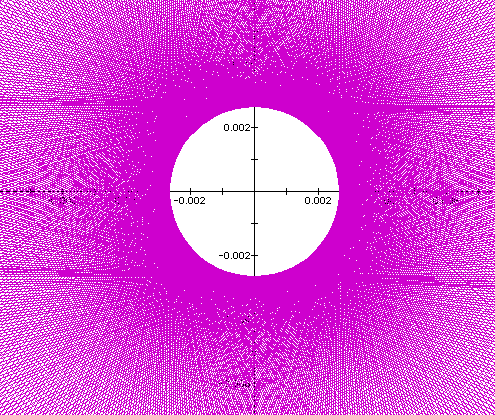
It turns out that the graph for the positive values of a and b are the same as the graphs for the negative values. Thus, this graph above is also true for a=b=300. It turns out that the circle closest to having the area filled is a=b=300 or a=b=-300. Let's test the values right around -300 to see if there is a limit.

Well, what happen is that -300<a or b<-299 gives us a function that does not have a circular form. There are also similar graphs between a,b=-299.9 and a,b=299.1, a,b=-299.8 and a,b=-299.2, a,b=-299.7 and a,b=-299.3, and a,b=-299.6 and a,b=-299.4. You could also explore further with more decimal places. What this does tell us is that a=b=300 and a=b=-300 are our limits for filling in the circular area of .

Case 2: a<b

for

x = cos (at)

y = sin (bt)

 

Let's look at some different values for a and b such that a<b.

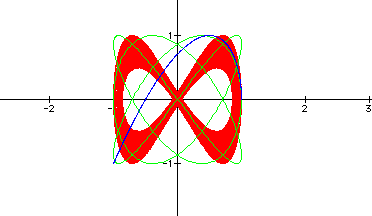
Above, we have a=3 and b=4 in the green, a=0.5 and b=0.75 in the blue, and a=100 and b=200 in the red. It appears that as the value of a is decreased the continuous function merges to one path.

Now, let's look at a constant a value and different b values. Below is a graph when a=5, b=10 in black and a=5, b=40 in the purple.

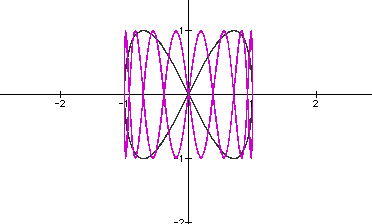
In most cases, when a is kept at a constant and b is increased, the function seems to have shorter periods in the "waves". Also notice that the function is bounded by x=1, x=-1, y=1, and y=-1.

Case 3: a>b

for

x = cos (at)

y = sin (bt)

 

Let's look at the graphs for a=10, b=5 in the black and a=40, b=5 in the purple.

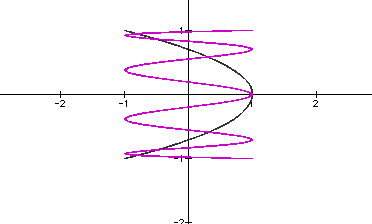
Comparing this graph to the last graph we looked at, when a>b the function is running horizontally. Above, when a<b, the function ran vertically. Also notice that the period is shortened as a increases.

Third Exploration

x = a cos (t)

y = b sin (t)

for t greater than or equal to 0 and less than or equal to 2 pie

 

In this exploration, we can study the cases, when a=b, when a<b, and whan a>b.

Case1: a=b

for

x = a cos (t)

y = b sin (t)

Let's look at a=1, b=1 in black, and a=2, b=2 in blue.

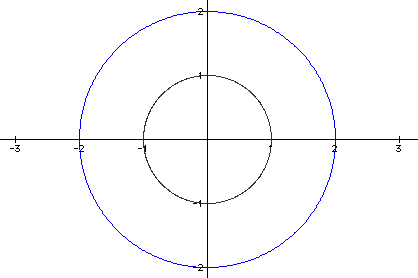
Notice that when a=b the value for a and b determines the radius. This is also the graph for a=-1, b=-1 in black and a=-2, b=-2 in blue. Therefore, the radius of x = a cos (t), y = b sin (t) is the absolute value of a or b when a=b.

Case2: a<b

for

x = a cos (t)

y = b sin (t)

 

Let's look at the graphs for a=2, b=5 in black, a=2, b=-5 in black, a=2, b=7 in blue, and a=2, b=-7 in blue.

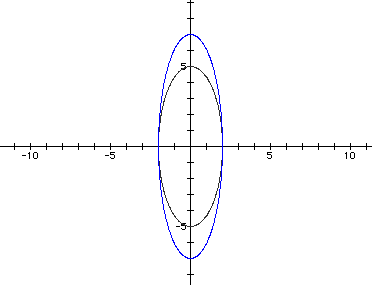
Here, we have an ellipse with a width of absolute value of a and a length with the absolute value of b.

Case3: a>b

for

x = a cos (t)

y = b sin (t)

 

Let's look at the graphs, a=4, b=1 in black, a=-4, b=-1 in black, a=8, b=1 in blue, and a=-8, b=-1 in blue.

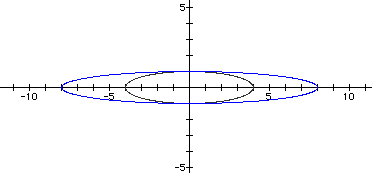
Here, we also have an ellipse with a width of absolute value of a and a length with the absolute value of b.

Return to Home Page