for less than or equal to 2 pie and greater than or equal to 0.

When a and b are equal, and k is an integer, this is one textbook version of the " n-leaf rose."

Let's graph a=b=2, k=1 (in black) and a=b=4, k=1 (in green).

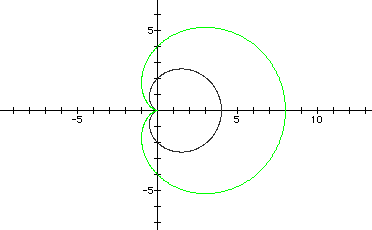
Notice that when a=b, a and b are scalar factors for the "n-leaf rose". Also, when k=1, the roots of

are 0 and a+b.

Next, we'll look at the effect of k on the equation. Below are the graphs of a=b=2, k=3 in black and a=b=4, k=5 in red.

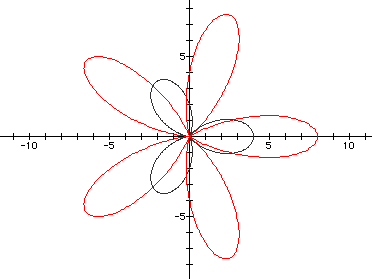
With these graphs and further exploration, we see that k determines the number of leaves in hte "n-leaf rose" figure.

Let's look at the graph of a=2, b=8, and k=1.

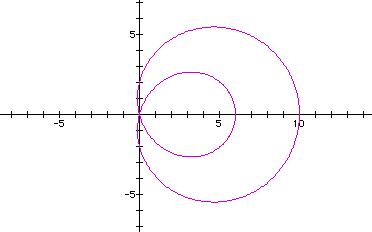
When a<b and k is an integer, will have roots at 0, a+b, and a-b. When a<b, the function traces a similar path to the "n-leaf rose" graph, but on a smaller scale. Thus, getting an inner "k-leaf rose". One inner "leaf"will always be at b-a on the x-axis.

Let's look at the graph of a=5, b=2, and k=10.

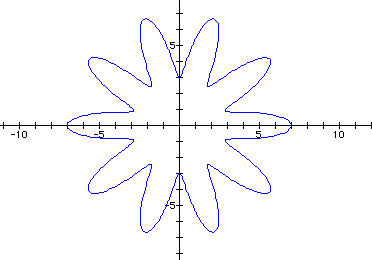
Notice that the "leaves" are merging towards a cirlce form. The leaves come in to a point on the circle centered on the origin with the radius a-b. The tips of the leaves work out to a point on the circle centered at the origin with the radius a+b. The function oscillates between these two circles k times to produce k "leaves".

Once you get to a large enough k, you can explore another characteristic of the graphs. Let's look at a=5, b=4.5, and k=2000.

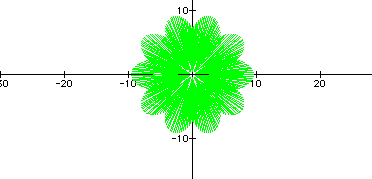
Now, if you look at this graph, you'll notice that the center is not filled. Let's take a closer look.

We get this graph by zooming in to the center of the graph. Notice that the inner points come to a "10-leaf rose". Also notice that 2000/200 = 10. With further testing and exploration, you will find that the graphs with k large enough will have a limit of a "k/200 - leafed rose".

Let's compare the graph of a=b=5, k=3 in green to a=b=5, k=3.4 in purple.

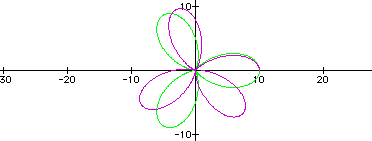
As you can see, the graph is no longer continuous. The graph is also merging towards the graph of a=b=5, k=4. So, the graph of is only continuous when k is an integer. In the graph above any k values between 3 and 4 will be noncontinuous functions between the "3-leaf rose" and the "4-leaf rose".

When a<b and k is not an integer, we see a similar transformation taking place as we see when a=b and k is not an integer. Let's look at the following graphs.

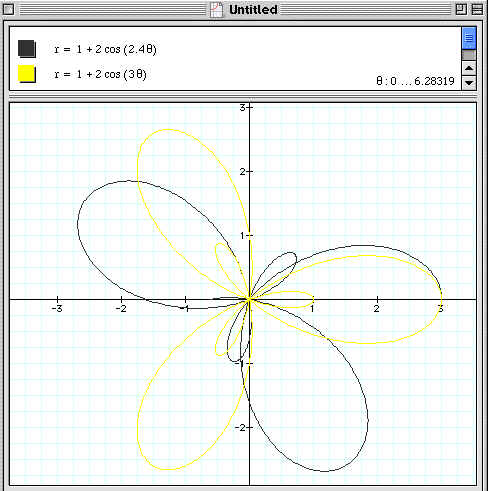
As you can see above, the graph when a=1, b=2, k=2.4 (in black) is not a continuous function and is looking more like the graph of a=1,b=2, k=3 (in yellow). So, as before, any k values between k1 and k2 will be noncontinuous functions between the "k1-leaf rose" and the "k2-leaf rose".

Well, what is your intuition this time? Are we going to see the same thing that we saw in the last two cases? Let's check your intuition by looking at the following graphs.

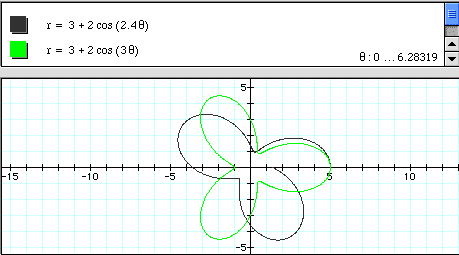
Look's like it is the same change that we have seen in the past two cases. As k is between k1 and k2, the function is noncontinuous and on it's way to becoming a "k2-leaf rose".

for less than or equal to 2 pie and greater than or equal to 0.

Click on the link below to see that n rotates the "petals" of the "k-leaf rose".

Since n rotates the graph of , n is the phase shift.

Return to Home Page