
Lesson 7:
3-Dimensional
Figures & Conics
By Carly
Coffman

Elliptical
Paraboloids
Many of the two-dimensional figures we look at,
come from cross sections of three-dimensional figures. We explored this in the first lesson when
discovering conics. Parabolas, Ellipse,
Circles, and Hyperbolas are all cross sections of a double cone. Now we will explore some other
three-dimensional figures and cross sections.
The first one we will look at is called an elliptical paraboloid. It is
formed by the equation, 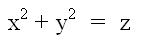 .
.
Notice that in three-dimensional figures there are three unknowns,
x, y, and z. Take a look (you can adjust
the values of x, y, and z on the right side):
Exploration 1
Open a Word Document, title it “Three-Dimensional Shapes”, and
type your name and date under the title.
Answer all questions in complete sentences.
1)
What are all of the possible two-dimensional cross sections that
can be formed from the elliptical paraboliod? (Make sure to include the equation)
Hyperbolic
Paraboloid
Now, let’s look at the hyperbolic Paraboloid. The equation, 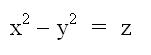 , forms a
hyperbolic paraboloid. Exploration
2
, forms a
hyperbolic paraboloid. Exploration
2
2)
What are all of the possible two-dimensional cross sections that
can be formed from the hyperbolic
paraboloid?
(Include the equation)
Look at the following cross-section: Exploration 3
Did you include this cross-section shape? If not, go back and include it in #2.
Other
Three-Dimensional Figures
3)
List the four three-dimensional figures and determine whether they
have cross-sections of parabolas, ellipse, circles, hyperbolas, or lines.
4)
Can you come up with any of your own three-dimensional figures or
find any on the internet? List equations
for any that you invent yourself or discover on the world
wide web. You can try them out by
typing them into the NuCalc link. NuCalc
Print your Word Document and file in
your portfolio or notebook. You have now
completed the three-dimensional exploration!
Return to
Home Page Next Lesson