
The
Tomahawk
Carly Coffman

When
looking through the book Geometrical Tools:
A Mathematical Sketch & Model Book by Robert C. Yates, I came
across a tool called the “Tomahawk”.
How to Construct The Tomahawk (using GSP 4.03)
1) Construct the semicircle BOC such that BO = OC
Ø
Using the
segment tool, construct segment BC (label endpoints B and C)
Ø
Highlight BC
and choose “Midpoint” under construct (label as point O)
Ø
Create segment
Ø
Highlight the
circle, point B, and point C, then choose “Arc on circle” under Construct
2) Construct a segment TB such that TB is tangent to
the segment BOC at point B.
Ø
Highlight
segment BC and the point B, then choose “Perpendicular line” under Construct
Ø
Highlight the
new line and choose “Point on the perpendicular line” under Construct : label
this point T
(You
can drag this point along the perpendicular line)
3) Construct segment AB on the end of BOC such that
AB = BO
Ø
Highlight
points B and O, then choose “Line” under Construct
Ø
Highlight
segment BO and point B, then choose “Circle by center+radius” under Construct
Ø
Click on the
intersection of line BO and the circle: label this point A
Ø
Highlight
points A and B, then choose “Segment” under Construct
4) Construct the end of the tomahawk
Ø
Highlight line
TB, then choose “Point on perpendicular line” under Construct : label this
point P
Ø
Highlight
point P and point A, then choose “Segment” under Construct
Ø
Move point P so
that angle BAP is about 28 degrees and point P lies on segment TB
Ø
Highlight
point P and point T, then choose “Segment” under Construct
5) Hide all lines and circles
Ø
Highlight all
lines (not segments) and circles, then choose “Hide Path Objects” under Display
6) Construct the handle of the Tomahawk
Ø
Highlight arc
BC, then choose “Point on Arc” under Construct
: label this point R
Ø
Move point R
so that it is closer to point B and the same distance as P away from segment AC
Ø
Highlight
segment TP and point R, then choose “Parallel Line” under Construct
Ø
Highlight
segment TP and point T, then choose “Perpendicular Line” under Construct
Ø
Click on the
intersection of the parallel and perpendicular line : label this point Q
Ø
Highlight
points T and Q, then choose “Segment” under Construct
Ø
Highlight
points Q and R, then choose “Segment” under Construct
Ø
Highlight the
lines, then choose “Hide Objects” under Display
Ø
You can adjust
the length of your handle by moving point T.
*An
extension would be to construct a curved handle at the end of the handle and a
curved segment AP.
7)
Hide the semi-circle and create arc RC
Ø
Highlight
segment BO and point O, then choose “Circle by center+radius” under Construct
Ø
Highlight the
circle, point R and point C respectively, then choose “Arc on Circle” under
Construct
Ø
Highlight arc
BRC and the circle, then choose “Hide Objects” under Display
* Another extension would be to construct
grooves in your tomahawk at points B and O.
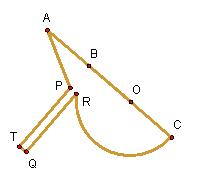
Congratulations,
you have created your own tomahawk!
*Challenge: Create the tomahawk for an angle starting
with your angle.
The Tomahawk Trisector
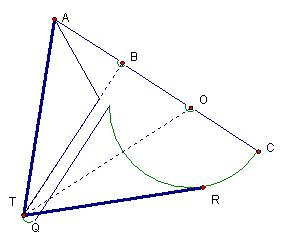
When
given any angle, you can use the tomahawk that we just created to trisect an
angle.
If
you adjust the tomahawk such that one ray of the angle runs through point A and
the other side of the angle is tangent to arc RC, the tomahawk trisects the
given angle. The three equivalent angles
are angle ATB, angle BTO, and the angle formed by the ray through points T and
O and the ray that passes through point T and O and the tangent point to arc
RC.
Click
here to manipulate the tomahawk and angle:
Trisector
Proof of why the the tomahawk works as an angle trisector:
For any
given angle, we can adjust the tomahawk such that one ray runs through points T
and A and the other ray runs through point T and is tangent to arc RC.
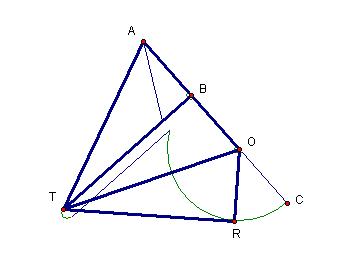
Since points
B and R are tangent points to circle O through point T, angle TBO and angle TRO
are right angles. Angle TBA is also a
right angle (*) since angle TBA is supplementary to angle TBO. So, we have three right triangles.
Since
segments
Since points
B and R are tangent points to circle O through point T, we also know that TB =
TR. By the reflexive property, TB =
TB. Thus, TB = TB = TR. Therefore, triangles TBA, TBO, and TRO are
congruent by the Side Angle Side theorem.
Angles BTA,
BTO, and RTO are congruent because Corresponding parts of congruent triangles
are congruent (CPCTC). Therefore, the
tomahawk is a tool for trisecting any given angle provided point A lies on a
ray of the angle and point R lies on a ray and is tangent to circle O through
point T.
The Tomahawk as a Cube Root Tool
(Proof
sketch found in Geometrical Tools: A
Mathematical Sketch & Model Book by Robert C. Yates)
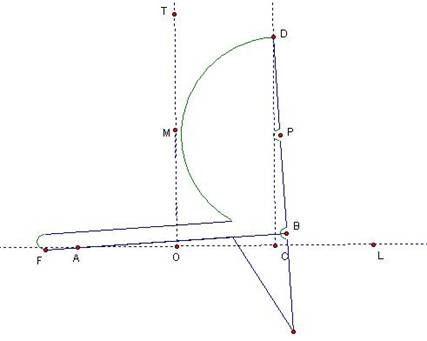
Cissoid of
Diocles
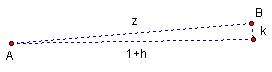
Corner D
moves along the fixed line CD while the outer edge BA passes through the fixed
point A, located 2 units from CD. The
path of the midpoint, P, of BD is the cissoid.
Proof that
point P forms the Cissoid:
Let AC be
the x-axis and its perpendicular bisector be the y-axis. BD = AC = 2 by construction and AB =
DC.
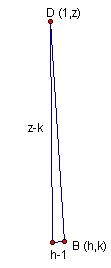
Let P =
(x,y), B = (h,k), D = (1,z).
Since P is
the midpoint of BD,
x = (1+h)/2
y = (z+k)/2
2x = 1+h 2y
= z+k
h = 2x-1 k
= 2y-z
In all
positions, AB = CD, so (1+h)2
+ k2 = z2
Substituting for h and k: (1+2x-1)2
+ (2y-z)2 = z2
4x2+4y2-4yz+z2=z2
X2+y2-yz = 0
X2+y2
= yz
z =
(x2+y2)/y
Then, since
AB is perpendicular to BD, their slopes are negative reciprocals. So,
Slope of AB = k/(1+h) Slope of BD =
(z-k)/-(h-1)
=
(-1)(k-z)/(-1)(h-1)
=
(k-z)/(h-1)
k/(1+h) = (-1)(h-1)/(k-z)
k/(1+h) = (1-h)/(k-z)
We can now
substitute with equations from above for k, h, and z :
h = 2x-1 k
= 2y-z z = (x2+y2)/y
h+1 = 2x k-z
= 2y-z-z
1-h = 1-(2x-1) k-z
= 2(y-z)
1-h = 2-2x
1-h = 2(1-x)
k/(1+h) = (1-h)/(k-z)
(2y-z)/2x = 2(1-x)/2(y-z)
(2y-z)/2x = (1-x)/(y-z)
2x(1-x) = (2y-z)(y-z)
2x-2x2=2y2-3yz+z2
Substituting for yz and z2 (from above) we
get:
2x-2x2=2y2-3(x2+y2)+[(x2+y2)/y]2
2x-2x2-2y2=-3x2-3y2+[(x2+y2)/y]2
Y2+x2+2x=[(x2+y2)/y]2
Multiply by y2: y4+y2x2+2y2x
= (x2+y2)2
y4+y2x2+2y2x
= x4+2x2y2+y4
0=x4+x2y2-2y2x
Divide by x: 0=x3+y2x-2y2
2y2-y2x=x3
Y2(2-x)=x3
Y2 = x3/(2-x) This is the equation of the
Cissoid of Diocles having
X=2
as Asymptote and cusp at (0,0).
Proof that
the Tomahawk creates a cube root of a given length:
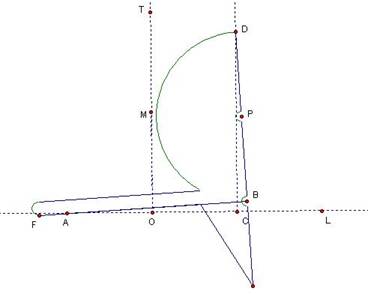
Let OL = 2
and its perpendicular
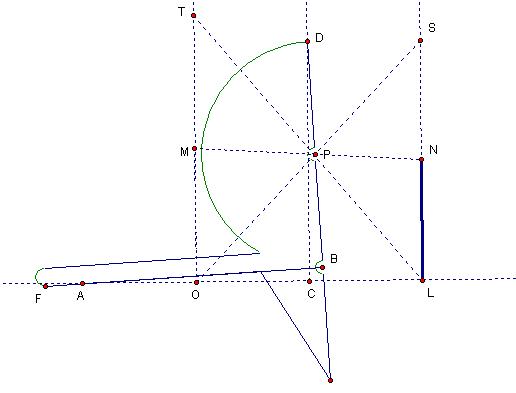
Remember
that P forms the Cissoid of Diocles (proof above) which has the equation Y2
= x3/(2-x).
Then, Y2 = x3/(2-x)
Y2(2-x)=x3
2y2-xy2=x3
Multiplying by y: 2y3-xy3=x3y
Y3(2-x)=x3y
Y3/x3=y/(2-x)
(y/x)3=y/(2-x)
Now, a line
OS runs through OP and has the equation,
y/x=m , since P is the point
(x,y).
So,
substituting m3=y/(2-x)
This
equation may also be thought of as the line through (2,0) and P(x,y), which is
the equation for the line LT.
The
y-intercept is OT = 2m3 since T is the point of intersection. Since LS = 2m and LN = LS/2,
(LN)3
=
So,
LN is the cube root or R, or OM. Thus,
the tomahawk produces the cube root of any given length.