Objectives:
1. to know the definition of perpendicular lines
2. to be able to write the equation of a line perpendicular to a given line
3. to understand and explain what makes lines perpendicular and their characteristics
Definitions:
Perpendicular lines are lines whose slopes are negative reciprocals of one another. The lines intersect to form right angles.
Negative reciprocals are two numbers that when they are multiplied together have product of -1.
This discussion is very similar to that of parallel lines, day 8. If one understood the discussion of parallel lines, one should not have any problems with perpendicular lines. The only difference between the two discussion is slope. The graphs are also different, but this is a consequence of the slopes being different, so we are going to think of this as only one difference.
First, recall the characteristic of perpendicular lines is that they intersect at a right angle. A consequence of this is that all four angles that are formed by the intersectionn are right angles. Graphically, perpendicular lines look like:

Remember, that just like with parallel lines, it does not matter what the y-intercept of either line is. They will remain perpendicular as long as their slopes are negative reciprocals. Click here for a movie that will change the y-intercept of the red line above. Notice, that as the red line moves, the two lines are still perpendicular.
Now, that we understand the basic characteristics of perpendicular lines and what they look like, it is time to understand what it means to be negative reciprocals. Negative reciprocals are two numbers that when they are multiplied together have product of -1.
To find the negative reciprocal of a number do the following.
Step 1. Write the number in the form of a fraction. If it is a mixed number, make it into an improper fraction.
Step 2. Reciprocate the fraction that was found in step 1. (Some people might call this inverting the fraction or just simply flipping the fraction over.) Basically, all we are doing is changing the places of the numerator and the denominator.
Step 3: Change the sign of the fraction that was found in step 2. So, if the fraction in step 2 is positive, the new fraction is negative or if the the fraction in step 2 is negative, the new fraction is positive.
Example1: Find the negative reciprocals of the given numbers.
a)
. The negative reciprocal is -3.
b)
. The negative reciprocal is
.
c)
. The negative reciprocal is
.
Example2: Are the following fractions negative reciprocals of one another? Explain why or why not.
a)
and
. Yes, they have different signs and they are reciprocals of one another, or because
. Either explanation is acceptable for this class.
b)
and
. No, they do not have different signs or because
equals 1 when it should equal -1.
You should now be able to determine whether or not two numbers are negative reciprocals of one another and be able to find the negative reciprocal of a given number. The next skill to develop is to be able to determine is two lines are perpendicular.
It was stated earlier that lines are perpendicular if there slopes are negative reciprocals. Recall, that the coefficient of the x-value is the slope, m, in the slope-intercept form of a line. In order to determine if two lines are parallel, we will apply the same logic as we did in example2.
Example3: Determine if the following lines are perpendicular.
This is a two step process. First, find the slopes of the two lines. Second, determine if they are negative reciprocals. This can usually be determined by looking at the slopes. If one can't do this by sight, multiply the slopes together. If the product is -1, then they are negative reciprocals. If the product is anything else, they are not negative reciprocals.
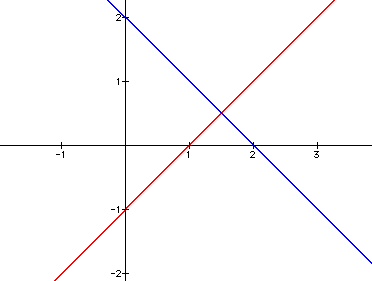
a)
and
. First, we find the slopes to be
and
. These are obviously negative reciprocals so the lines are perpendicular. This can also be seen graphically by:
.
b)
and
. Here the slopes are
and
. These are not negative reciprocals because there product is 1 instead of -1, so the lines are not perpendicular. This can alse be seen graphically below.
.
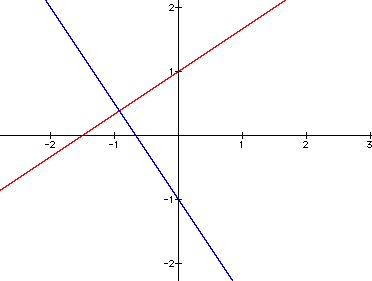
Note: Do not rely on graphing to determine if lines are perpendicular. It is possible to graph lines that appear to be perpendicular that are actually not perpendicular. For example, are the lines graphed below perpendicular?
Just looking at the graph, it would be reasonable for one to
believe that the lines are perpendicular, but the equations of
the lines graphed above are:![]() in
red and
in
red and ![]() in blue. Now that
we have the equations, it is easy to see that in fact the lines
are not perpendicular.
in blue. Now that
we have the equations, it is easy to see that in fact the lines
are not perpendicular.
Finally, we are ready to write the equation of a line that is perpendicular to a given line. This will work exactly like writing the equation of a parallel line.
First, we must determine the slope of the of the perpendicular line. We have already learned how to do this because the new slope is the negative reciprocal of the slope of the given line.
Second, we choose between point-slope and slope-intercept form. Remember, this decision is based on the given point. If the point gives us the y-intercept, we use slope-intercept form. If not, we use the point-slope form.
Third, substitute in our values for and solve the equation for y.
Examples 4 and 5 will walk you through writing the equation of a line perpendicular to a given line.
Example4: Write the equation of a line through the point (0,2) and perpendicular to y = 2x - 1.
Step 1: Determine the slope of the perpendicular line.
The slope of the given line is 2. So, the negative reciprocal of 2 is
.
Step 2: Choose between point-slope and slope-intercept form.
The point (0,2) tells us that our y-intercept (b) is 2. So, we choose slope-intercept form, y = mx + b.
Step 3: Substitute for m and b and solve for y.
Substitution gives us the equation,
, which is the equation of the perpendicular line that we are looking form.
Just to check and see if they look write, we will graph the two lines.
The graphs appear perpendicular, so we feel confident that we have done the work correctly.
Example5: Write the equation of a line through
the point (-3, 2) that is perpendicular to the line, ![]() .
.
Step 1: Determine the slope of the perpendicular line.
The slope of the perpendicular line is the negative reciprocal of
which is
.
Step 2: Choose between point-slope and slope-intercept form.
The point (-3, 2) does not tell us what the y-intercept is so we must use point-slope form, y - y1 = m(x - x1).
Step 3: Substitute for m, x1, and y1 then solve for y.
This gives us the equation,
. Next, distribute to get:
. Finally, add 2 to both sides to find the equation of the perpendicular line to be:
. Again, as a check, we will graph the two lines to see if they look perpendicular.
.
Again, they apppear perpendicular so we can feel confident that we have found the correct line.
Now, you should be able to complete all of the work that we are going to do with perpendicular lines.