Think back to Algebra I. We learned about lines and how to graph them. During Algebra I, we found three general forms of lines. They are:
1. Standard Form: Ax + By = C
2. Slope-Intercept Form: y = mx + b
3. Point-Slope Form: y - y1 = m(x - x1)
When solving systems of linear equations graphically, we use the same concepts as we did to graph individual lines in Algebra I. The only difference in that we will graph two lines on one coordinate plane.
So, this becomes a very simple process when using a program such as graphing calculator. This program can accept any form of the line and graph it. It is a little more difficult when using a TI-83 because the line needs to be in slope-intercept form.
So, first we will look at how to find the solution graphically regardless of form. Then, we will look at how to use the TI-83 to find the answer graphically.
When doing the examples, you will be asked to do them as I do them. This is so that you can learn the correct keystrokes on your calculator.
Step 1: Hit the Y= button. The screen on your TI-83 should now change and you should see Y= along the left hand side. This is the screen where we will type in the equation of the line.
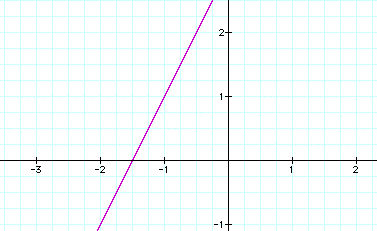
Step 2: Type in the equation of the line. So, pretend you are given the equation y = 2x + 3. The y= portion of the equation is already taken care of for you. So, all one has to enter is the 2x + 3 portion. So, to do this, hit the number 2 then to get the x hit the alpha key followed by the sto key. The sto key is directly above the on key or the second key from the botton on the left hand side. Finally, hit the plus key and the three key and you should see the equation y = 2x + 3.
Step 3: Hit the graph key and the screen should change to show you the graph of the equation. Your graph should look like this:

Note: To graph two lines at the same time, a person must do step 2 twice before hitting the graph key. So here, there will be an equation next to Y1 and Y2.
To find the answer graphically, all one has to do is find the point of intersection of the two lines. This is the one point in the plane that will make both of these equations true.
We will start by looking at three examples of lines in slope-intercept form and then look at an example with lines in standard form and also an example with the lines in point-slope form.
The directions for all of the examples are to find the solution to each system of equations graphically. Or, in other words, find the point of intersection of the two lines.
Example 1: Two lines in slope-intercept form.
Find the solution for the lines: ![]() and
and
![]() .
.
Type these both into your Ti-83 and hit graph. Click on the link below to see if your graph is correct and to see the answer.
Example 2: Two lines in slope-intercept form.
Find the solution for the lines: ![]() and
and ![]() .
.
Example 3: Two lines in slope-intercept form.
Find the solution for the lines: ![]() and
and
![]() .
.
Example 4: Two lines in standard form.
Find the solution for the lines: ![]() and
and
![]() .
.
Here, you will have to solve both of these for y before typing the equations into your calculator.
Example 5: Two lines in point-slope form.
Find the solution for the lines: ![]() and
and
![]()
Here, you will have to solve both of these for y before typing the equations into your calculator.
1. Parallel Lines: Two lines are parallel when the have the same slope. When lines are parallel, they never intersect so there is no solution for the system of equations. This is called inconsistent.
Example:
Notice that the both have the same slope of 2 so these lines are parallel. Thus, the answer is no solution.
2. Same Line: Two equations may be the same line just in different forms. When this happens all real numbers make the system true and this is called dependent.
Example:
Notice that there is only one line and it is black. The red equation is just the purple equation multiplied by 2. Therefore, they are the same line and the solution is all real numbers.