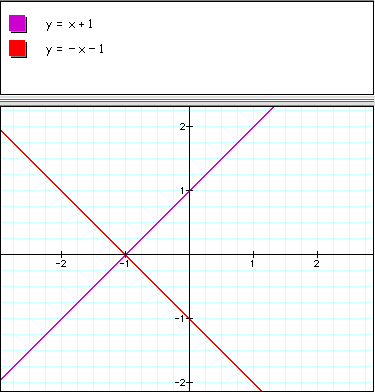
This is very similar to solving systems of equations, topic 3. The only difference is that the equal sign will be changed to an inequality sign. Instead of looking for a specific point of intersection as our answer, we will be looking for a region (area) of the graph that gives all of the points that will make the system of inequalities true.
For example, we have already seen how to solve problems like the one below.

Now, we will try to solve when we change the equal sign to an inequality sign. First, recall a couple of ideas. One, that the line is dotted when the inequality is less than or greater than, and the line is solid when the line is less than or equal to or greater than or equal to.
Look at the example below.
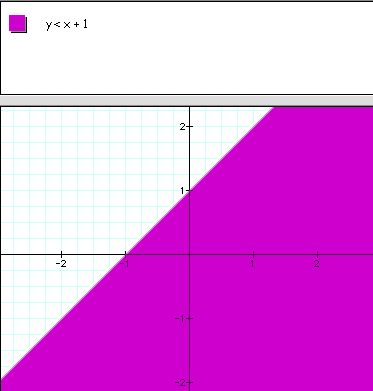
Do you see a problem with how the computer graphs the inequality? Based on the equation y < x + 1, the line should be dotted. The computer program just uses the line as a boundary, but does not take into account whether the boundary is part of the solution set or not. So, when graphing theses inequalities using technology, one must pay close attention to the boundary lines.
So, now that we see how to graph one inequality, finding the solution to a system of inequalities becomes very easy. We graph two inequalities on the same coordinate plane and find where the shaded regions intersect instead of just a point of intersection.
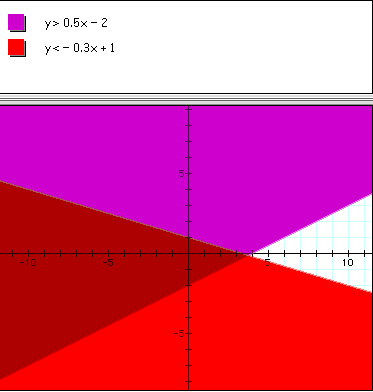
For example: We tale the lines from above and change bothe equal signs to less th an signs.

So the solution is the region that looks like a deep shade of red. That means that any point in that region will make both inequalities true. So, lets look at one more.
Here again, the dark red area is the solution set to this system of inequalities. Now, how do we use the TI-83 to solve systems of inequalities.
This is very similar to what happens on the computer program graphing calculator. Just like the computer, the TI-83 will not show the line as solid or dotted. You will have to take care of that. So, here are the steps:
Step 1: Hit theY= key. The screen should now look like \Y1= .
Step 2: Use the arrow keys to move the cursor onto the backslash (\) in front of Y. The slash should now be blinking.
Step 3: Use the enter key to cycle through the different options. When one hits enter, the backslash will change. We change this to get the TI-83 to shade the graph.
Greater Than: looks like a solid arrow pointing upwards.
.
Less Than: looks like a solid arrow pointing downwards,
.
Now, let's try one together. Use your TI-83 to find the solution to the following system of inequalities.
![]() and
and ![]() .
.
Does your answer look like this?
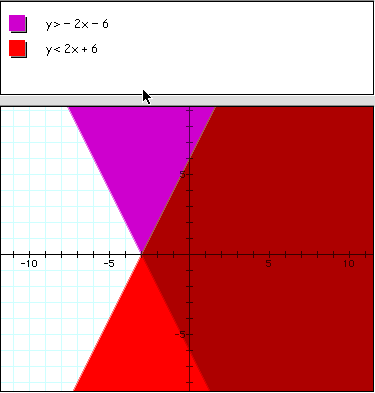
We should now be able to solve systems of Inequalities.
Bonus: