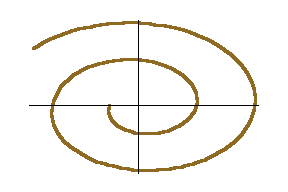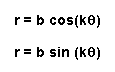
for various b and k.
by
Behnaz
Rouhani
In this assignment we are going to investigate the following polar equation cases.
Case I:
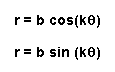
for various b and k.
Case II:
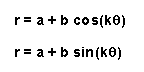
for various a, b, and k.
Case III: Special investigation
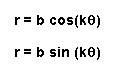
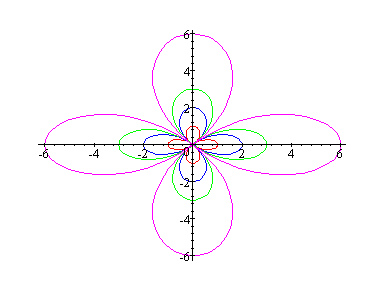
b = 1 : red
b = 2: blue
b = 3: green
b = 6: magenta
![]()
![]()
Notice that multiplying the above two graphs by a factor of b causes the graphs to become larger by a factor of b. In these graphs the sine polar curve is symmetrical about the vertical line, whereas the cosine polar curve is symmetrical about the polar axis (horizontal axis). When k = 2, we have a 4-leaved rose.
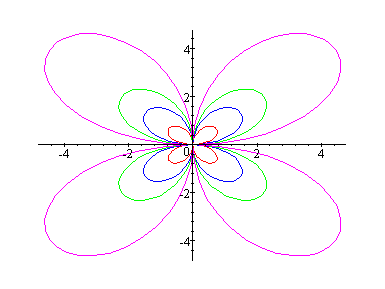
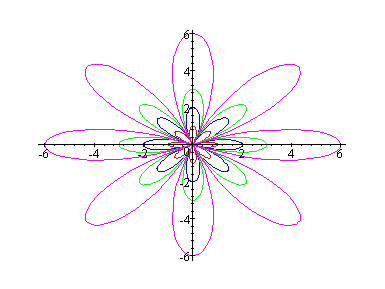
Let's see what happens when k = 4.
![]()
![]()
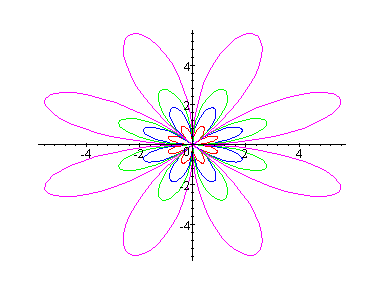
In the above sine and cosine graphs when k = 4, we have 8 petals. Based on the above graphs we could conclude that:
b = 1 : red
b = 2: blue
b = 3: green
b = 6: magenta
![]()
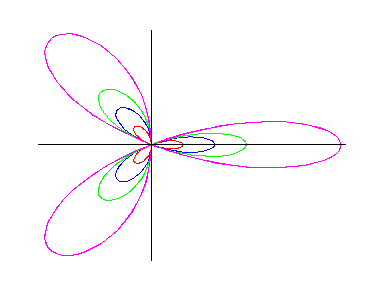
![]()
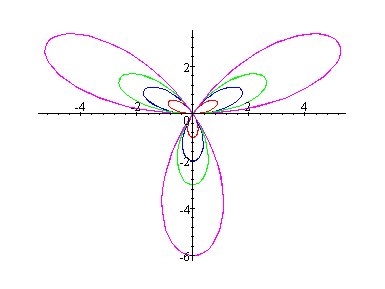
From the above graphs we could conclude the following:
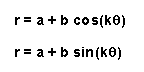
Different values of a and b are represented in the following graph.
a = b = 1: red
a = b = 3: blue
a = b = 6: magenta
Consider k=1 ----this is graph of Cardioid.
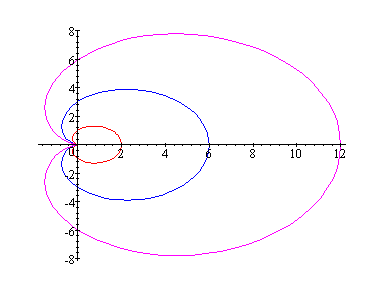
This curve is called Cardioid because
it is shaped like a heart. This polar curve is symmetrical about the polar
axis (horizontal axis).
Consider k = 2
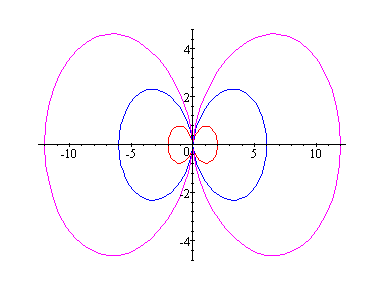
This polar curve is symmetrical about
the vertical axis.
Consider k = 3
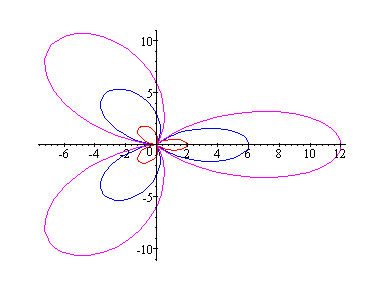
From the above we can make the following observations:
Different values of a and b are considered in the following graphs.
a = b = 1 : red
a = b = 3: blue
a = b = 6: magenta
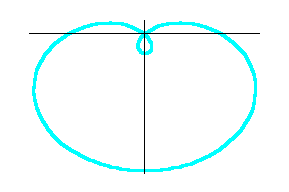
Let k =1 --- case of a Cardioid
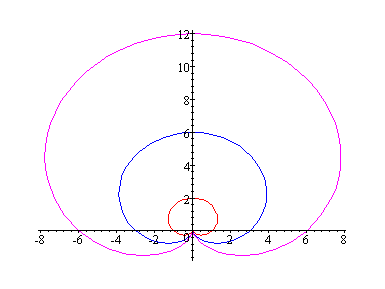
This polar curve is symmetrical about
the vertical axis.
Let k = 2
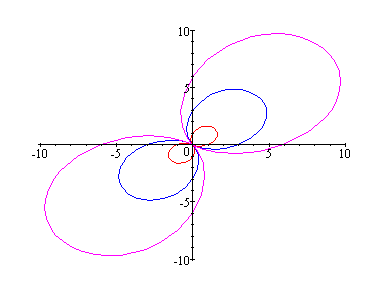
This polar curve is symmetrical about
the pole.
Let k = 4
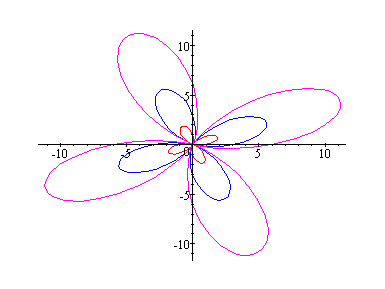
As we vary a = b, the graph just gets larger by that factor. For instance when a = b = 3, then the graph gets larger by a factor of 3. In this case the number of petals is same as k.
![]()
Following are graphs of a Limacon.
![]()
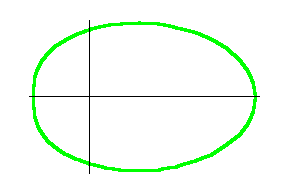
![]()
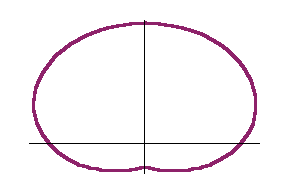
![]()
![]()
![]()
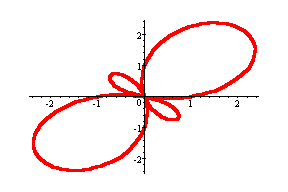
![]()
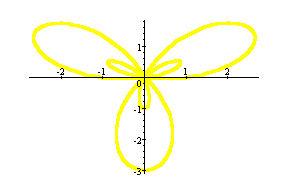
![]()
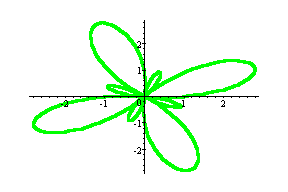
In all the above cases whether k is odd or even we
get 2k petals half of which are small and half are large. The only difference
is that when k is odd the small petals are inside the large ones, but when
k is even the small petals are outside the large ones.
This following is the graph of a spiral.
![]()