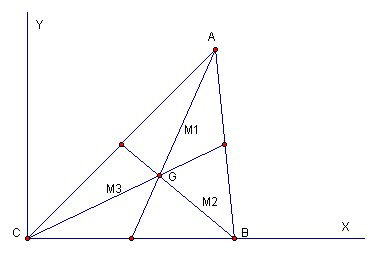
The centroid of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.

In this assignment we prove that the three medians are concurrent at the centroid. In the figure below all three medians are shown with dotted lines, and the centroid is denoted as G.

If we explore this idea of centroid, and use Geometer's Sketchpad, we will come to notice that the medians of a triangle are inside the triangle, and thus their intersection, the centroid is also an interior point of the triangle. It remains to be proven that the medians meet at the same point.
 

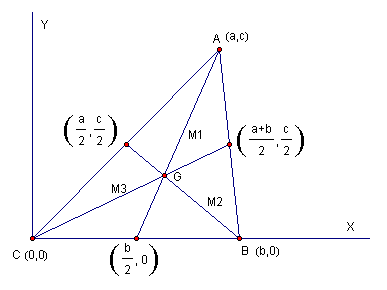
To make this case easy to comprehend we will assume that this triangle is in the first quadrant of the Cartesian plane, and that one of the vertices is located at the origin. Therefore, the coordinates of the vertices of the triangle are given as below. Further,  the midpoint of each side of the triangle is found using the midpoint formula. Given the coordinates of the end points of a line we could find the midpoint by taking the average of the x- and y-coordiantes of each endpoint.
 
 

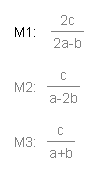
The slopes of the three medians are given as:

The equations of the medians are given as:

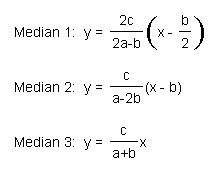
Now, the question is whether the point of intersection of these three lines will be one point. To test this, we will find the point of intersection of any two lines at a time. Then, if we find that the point of intersection for any of the two lines we have considered has the same coordinates we can conclude that the medians are concurrent at the centroid.

The point of intersection of M1 & M2:

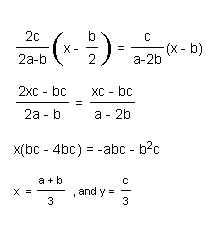
The point of intersection of M2 & M3:

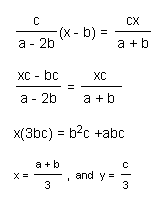
Similarly, the point of intersection of M1 & M3 will also be the point

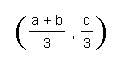
Based on the above it is concluded that the three medians meet at the centroid.