In this assignment we are going to investigate the following problem:

Given two circles and a point on one of the circles, construct a circle tangent to the two circles with one point of tangency being the designated point .

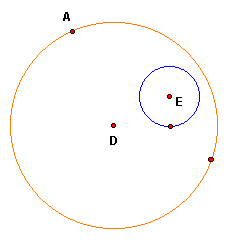
We are given circles D and E, and point A on circle D. The plan is to construct a circle tangent to both circles with the designated point of tangency. Let us consider the following two cases:

Case A: two circles are disjoint

• Smaller circle is inside the larger one
• Smaller circle is outside the larger one

Case A1: Two circles are disjoint --- smaller circle is inside the larger one

 First, we will construct a line through point A and center D. Then, construct a circle with center A and radius equal to that of circle E.

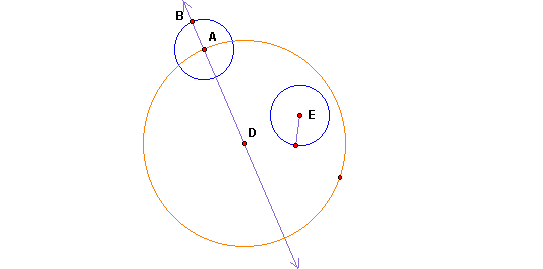
Next, we will connect points E and B (this segment will be the base of the isosceles triangle). Then, construct a perpendicular line through the midpoint of BE. The vertex of the triangle (point H) is where the perpendicular line and the line through B&D intersect. This point is also the center of the tangent circle.

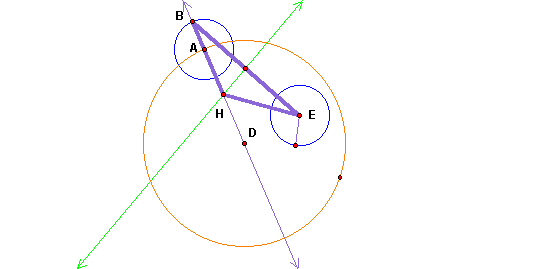
 Finally, we will construct a circle with center at H and radius AH. The black circle shown in figure below is the constructed tangent circle to both circles D and E.

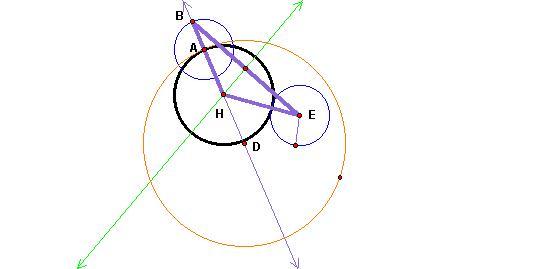
As point A moves around circle D, the locus of the center of the tangent circle H traces out an ellipse (shown in brown). The foci of the ellipse are the two centers of the given circles D and E. To animate the graph and see the ellipse traced, click here.
 
 

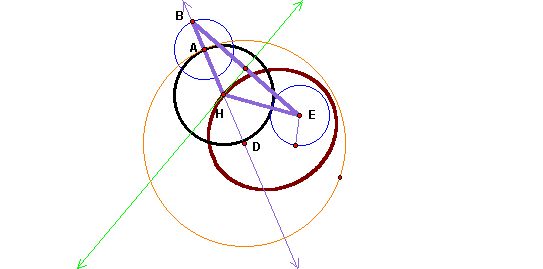
It is worth noting that distance HD + HE = radii of circles E & D. The green line in the construction is always tangent to the ellipse. To see how envelope of lines are produced as the point A moves around the large circle click here , to do so, trace the tangent line (shown in green).

Case A2: Two circles are disjoint --- smaller circle is outside the larger one

In this case the smaller circle is outside the larger one. The construction of the tangent circle is just like the case discussed above. The tangent circle (shown in black) is centered at H with radius AH. The locus for the center of the tangent circle is a hyperbola (shown in brown) with its foci located at the center of the circles D and E.
 
 

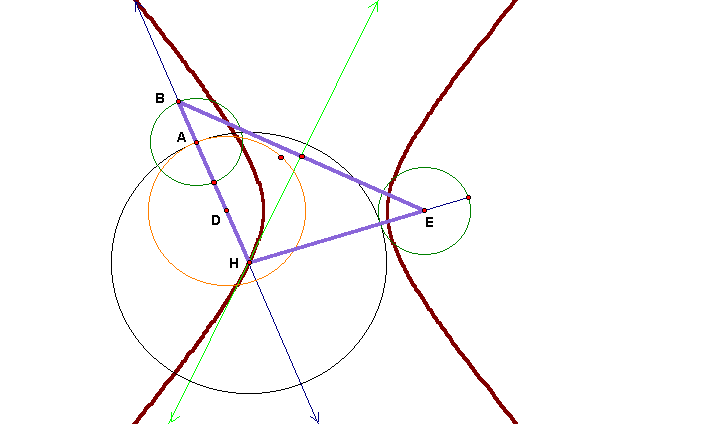
Now, to see how the hyperbola is traced click here. If we trace the tangent line (green line) as point A is animated around the tangent circle, then we will see an envelope of lines that are all tangent to the hyperbola. Click here to see the animation.

Case B: Two circles intersect

The final case under consideration is when the two circles intersect. In this case the tangent circle (shown in black) and the locus for the center of the tangent circle (shown in brown) is a circle with center at D.

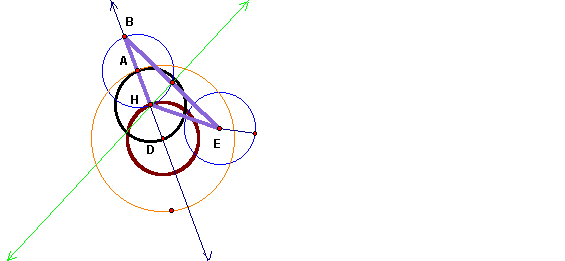
The tangent circle exploration has lots of topics to be investigated. In this assignment we have only touched upon few cases of tangent circles. Hopefully this will be a start for further investigation.