Assignment 8

Altitudes and Orthocenters

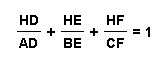
by

Behnaz Rouhani

Given that ABC is an acute triangle, construct the orthocenter H. Let Points D, E, and F be the feet of the perpendiculars from A, B, and C respectively.

Prove that:

Case I:

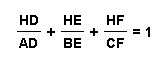
Case II:

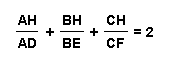
We should consider what happens if ABC is an obtuse triangle, and see if the above relationships still hold.


Triangle ABC is acute

First, we would construct the orthocenter H of triangle ABC, and let the points D, E, and F be the feet of the perpendiculars from A, B, and C respectively.

Case I:

We know that

area (ABC) = area (HAB) + area (HAC) + area (HBC)

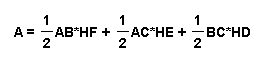
Now, divide both sides of the above equation by A, to get:


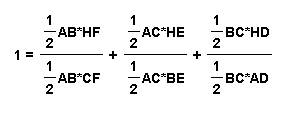
After simplifying the fractions we get:


or

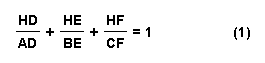
Case II:

To find the validity of the second case we know that:

HD = AD - AH
HE = BE - BH
HF = CF - CH
In equation (1) substitute the above relationships for HD, HE, and HF, to get:

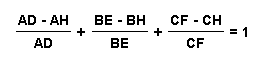
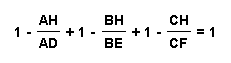
Rearrangement of terms gives



Triangle ABC is obtuse

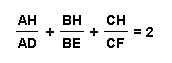
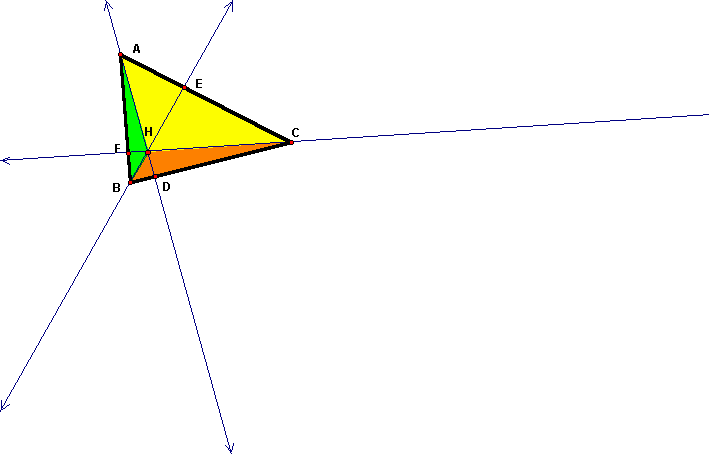
When we have an obtuse triangle the orthocenter will be outside the triangle. In the figure below the orthocenter of triangle ABC is constructed. Then feet of the perpendiculars from vertices A, B, and C are points D, E, and F respectively.


 
 

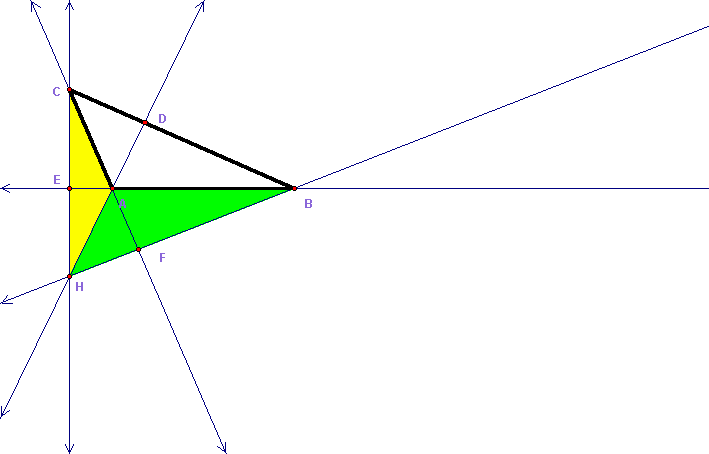
Case I:

In this case

area (BCH) = area (ABC) + area (AHB) + area (CAH)


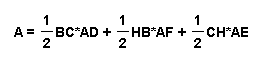
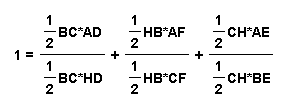
After simplifying fractions we get:

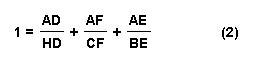
As we can see this is different from equation (1) which we proved earlier.

Case II:

To prove the second relationship, we know that:
 

AD = HD -AH
AF = CF - CA
AE = BE - AB
Now, if we substitute the above relationships for AD, AF, and AE in equation (2) and rearrange the terms then we get:
 


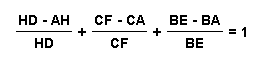
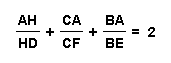
Do you see any similarities between the relationships for the acute and obtuse triangles?


Return to Behnaz Rouhani's Page