The Pythagorean theorem is one of the earliest theorems. This famous theorem is named after the Greek mathematician and
Philosopher, Pythagoras. Although the theorem was named after him but there is evidence that the Babylonians knew this relationship some 1000 years earlier. Plimpton 322, a Babylonian mathematical tablet dated back to 1900 B.C., contains a table of Pythagorean triples. The Chou-pei, an ancient Chinese text, also provides the evidence that the Chinese knew about the Pythagorean theorem many years before Pythagorean.

The Pythagorean Theorem is Pythagoras' most famous mathematical contribution. According to the legend, Pythagoras was so happy when he discovered the theorem that he offered a sacrifice of oxen. The later discovery that square root of 2 is irrational
and, therefore cannot be expressed as a ratio of two integers, greatly troubled Pythagoras and his followers.

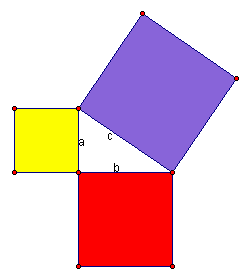
The Pythagorean theorem states that: "The area of the square built on the hypotenuse of a right triangle is equal to the sum of the squares on the remaining two sides."
 

According to the Pythagorean Theorem, the sum of the areas of the red and yellow squares is equal to the area of the purple square.

Thus, from the theorem we have the following relationship:

Area of red + Area of yellow = Area of purple

There are many proofs for the Pythagorean Theorem. Here we will only take a look at four of such proofs:

Choupei’s Proof

The following figure is made up of a large square, small square and four right triangles.
 
 

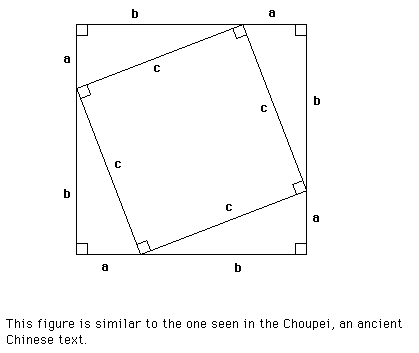
The steps of the proof are as follows:

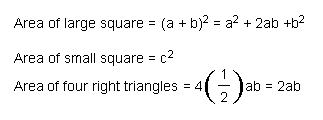
As the large square consists of one small square and four right triangles, thus we can write

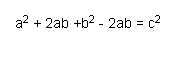
Or

Therefore, the sum of the squares of the sides of a right triangle equals the square of the hypotenuse.

Bhaskara's first Proof

Bhaskara was born in India. He was one of the most important Hindu mathematicians of the second century. In the following diagram the three right triangles are congruent, and the large square is made up of a small square and four right triangles.

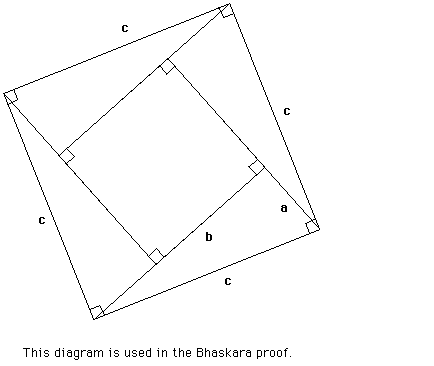
From the above figure:

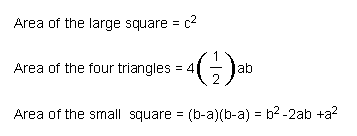
Now, the area of the large square consists of the area of the four right triangles plus the area of the small square. Thus,

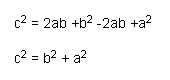
Bhaskara’s second Proof

In this proof Bhaskara began with the right triangle ABC, then he drew the altitude AD.

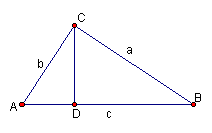
Bhaskara used the property of similar triangles to prove the theorem. In here the triangles ABC, BCD, and ADC are similar. Thus, we could write the following:

When we consider triangles ABC and ADC we can conclude:

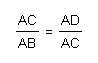
And, when we consider triangles ABC and BCD we can conclude:

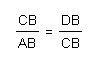
Next, we will cross-multiply the ratios obtained above to get:

Finally we will add the left –hand side of the above products together and the right-hand sides together to get:

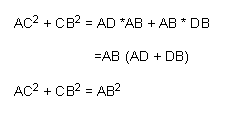
Or

Garfields Proof

President James A. Garfield discovered this proof in 1876. As opposed to the other proofs, here we draw no squares, but simply use algebra to prove the theorem.

Garfield used the following trapezoid to develop his proof. The way this proof works is to find the area of a trapezoid two different ways, and then equate those areas. As we can see this trapezoid consists of three right triangles.

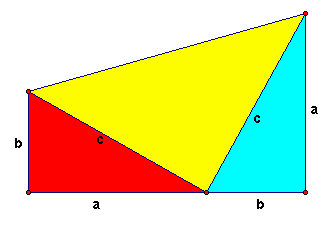
Area of a trapezoid is given by:

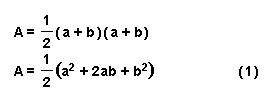
We can also find area of the trapezoid by summing up the areas of the three right triangles:

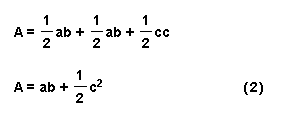
Now, in equations (1) and (2) their left-hand sides are equal, therefore,

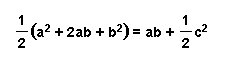
By multiplying both sides of the above equation by 2 we will get

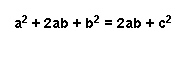
After further simplification, the above equation yields,