Given any triangle ABC, we can construct equilateral triangles on each side of this triangle, then connecting the centers of each equilateral triangles would result in the Napoleon's Triangle JKL. Since in an equilateral triangle all centers, namely, centroid, orthocenter, incenter, and circumcenter are all concurrent, therefore, it is only necessary to find one of the centers.

Now, we will investigate Napoleon's Triangle given different types of triangles. Let us consider the following cases:

Case - 1: Original Triangle (ABC) is a scalene triangle

Case - 2: Original Triangle (ABC) is a right triangle
 

Case - 3: Original Triangle(ABC) is an isosceles triangle
 

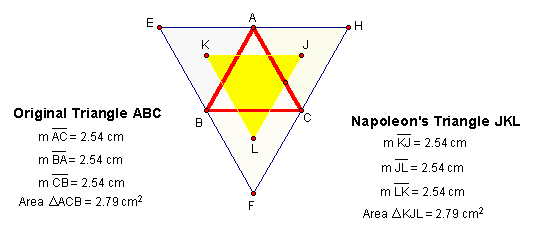
Case - 4: Original Triangle (ABC) is an equilateral triangle

The areas of all the triangles constructed on the sides of the original triangle are the same:

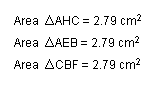
As we can see in all of the above cases, the Napoleon's triangles are equilateral triangles. Another interesting observation is that when the original triangle is equilateral, the area of the Napoleon's Triangle, JKL, is the same as the area of the original triangle. Or,

The Napoleon's Triangle we have been investigating so far is the outer Napoleon's Triangle. We can also construct inner Napoleon's Triangle. To do so we will reflect each of the centers J, K, and L across their corresponding edge in the original triangle ABC. This would result in the inner Napoleon's Triangle J'K'L'.
 

It looks like for the triangle ABC (right triangle) the inner Napoleon's triangle is an equilateral triangle. Further,

This conjecture proves to be true for any kind of a triangle. Could you show that this is true? If in doubt click here and see it for yourself.

Return to Behnaz Rouhani's Page