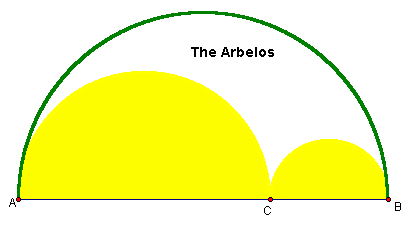
The term "arbelos" means shoemaker’s knife in Greek, and this term refers to the white region in figure below. This also resembles the blade of a knife used by ancient cobblers.

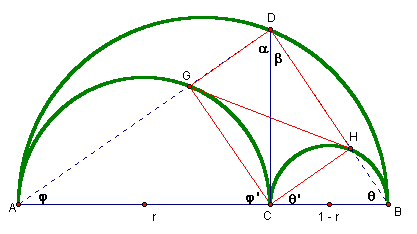
In order to observe the behavior of the arbelos, click here for a GSP sketch, where you can drag point C along diameter AB. Given the arbelos as described above, construct a perpendicular to AB at C, so that it intersects the semicircle with diameter AB at D. Next, construct the intersection of the segment AD and the semicircle with diameter AC and call the intersection G. Finally, construct the intersection of the segment DB with the semicircle with diameter BC and call it H. Now, we would like to prove that equilateral HCGD is a rectangle.
 

Triangle ADB is inscribed in a semicircle, and its hypotenuse is the diameter of the semicircle, thus triangle ADB is a right triangle.
 

Also, triangle DCB is a right triangle and by definition we know that

Triangle DAC is a right triangle and by definition,

From equation (3)

Now, substitute equation (4) into equation (1) and get

Similarly,

Triangles AGC and BHC are inscribed in semicircles and their hypotenuses are diameters of the semicircles. These triangles are right triangles, and angles AGC and CHB are right angles. Therefore,

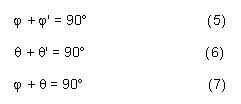
From equation (7)

Now, substitute equation (8) into equation (5) and get

Similarly,

By angle addition,

The two triangles DGC and DHC are congruent by ASA. Since corresponding sides of the congruent triangles are congruent, it follows that HC = GD and DH = GC. Also, angle GCH is a right angle by addition. Therefore, the equilateral DGCH is a rectangle.

The arbelos satisfies a number of identities. In here we will attempt to address few of those:

1. Arc length along the enclosing semicircles is the same as the arc length along the two smaller semicircles, or
Arc length AKB = Arc length AEC + Arc length CFB.

To prove this let us look at the following figure.

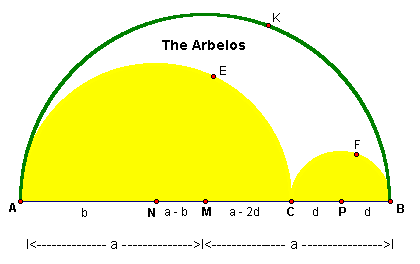
As noted in the above figure, M is the center of the semicircle AKB, N, is the center of the semicircle AEC, and P is the center of the semicircle CFB. From the above figure, since AM = a, and AN = b, hence NM = a – b.

Next, in the smaller semicircle we let CP = d, therefore, MC = a - 2d. We know that circumference of a semicircle is C = p r. Therefore:

Arc length AKB = p a                    (9)

Arc length AEC = p b                   (10)

Arc length AFB = p d                   (11)

Also from the above figure we know that,

NM + MC = AN

(a – b) + (a – 2d) = b

2a – 2d = 2b

or

2a = 2d + 2b ===è a = d + b

Now, using the information from (10) and (11):

AEC + AFB = p b + p d = p (b +d ) = p a = AKB

2. The area of the circle with diameter DC is the same as the area of the arbelos.

In this section draw the perpendicular DC from the tangent of the two semicircles to the edge of the largest semicircle. Then, we want to claim that the area of the circle with diameter DC is the same as the area of the arbelos.

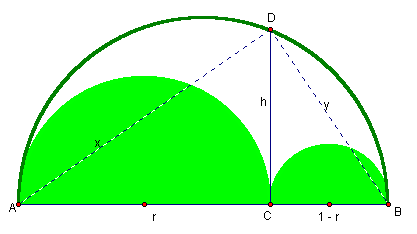
In here we let AB = 1, and AC = r, then from the above figure we can write

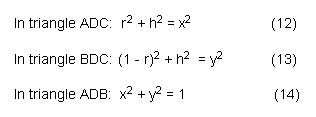
We solve equations (12) and (13) simultaneously, and after much simplifications we get equation (15).

Or

Substitute equation (15) into equation (14) to get:

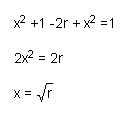
Next, we substitute the above expression for x into equations (15) and (12), and find corresponding expressions for y and h.

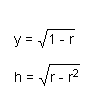
After this preliminary work we could proceed with the proof, and for that we look at the figure below:

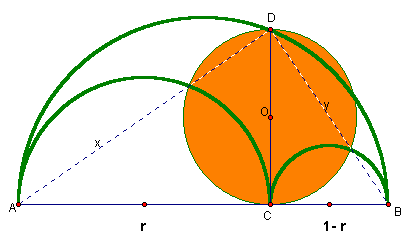
We know that radius of the circle with center at O is

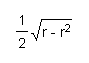
Therefore, the area of  the circle with center at O is

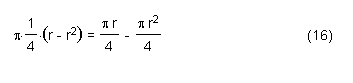
From the above figure we can tell that the area of the arbelos is:

Area of the semicircle with diameter AB – Areas of the semicircles with diameters AC & BC.

Thus, we can write,

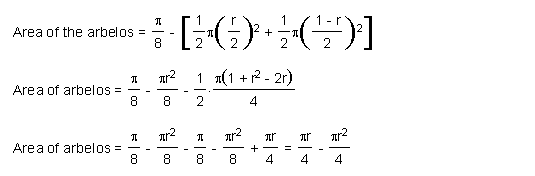
Therefore, area of the arbelos is the same as the area of the circle with diameter DC as shown in equation (16).