by
Behnaz
Rouhani
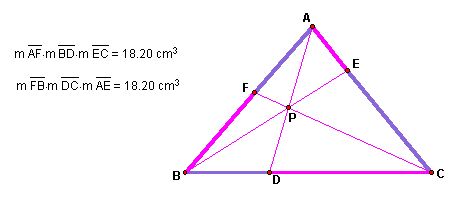
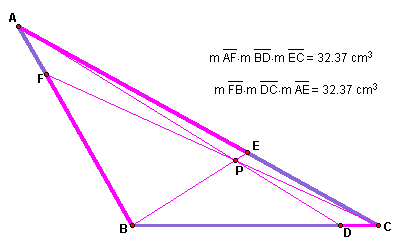
The products appear to be equal for any triangle ABC and for any position of P. Below are two sketches for acute and obtuse triangles.
Acute triangle

Obtuse triangle
To explore this further with different types of triangles
and different positions of P click
here.
To prove that the products of the segments must be equal, we will draw some parallel lines to AD from C and B. Extend CF to intersect the parallel line at S and extend BE to intersect the other parallel line at R as shown below.
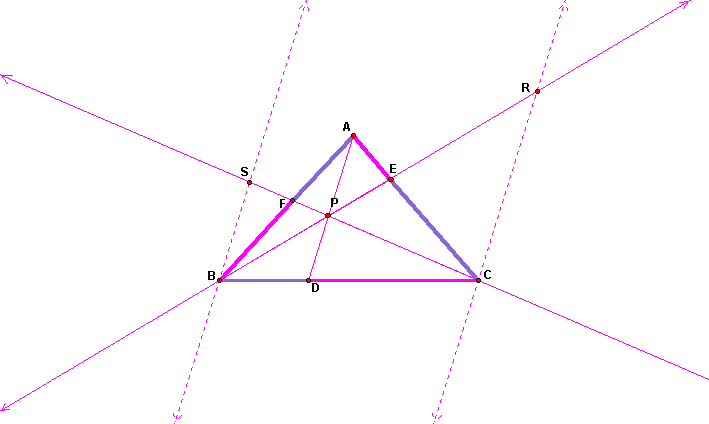
Now, we have several similar triangles. These four
pairs of similar triangles are important for the proof:
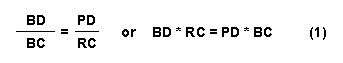
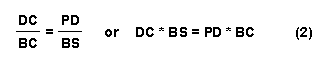
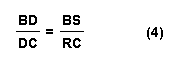
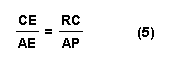
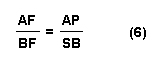
Multiplying the left-hand sides of equations (4),
(5), and (6) and multiplying the right-hand sides of the same equations
together would yield:
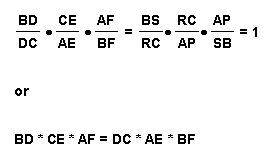
This is the proof of the first part of Ceva's Theorem which states that in a triangle ABC, three lines AD, CE, and BF intersect if and only if
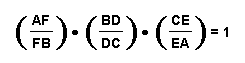
This result can be generalized for points outside the triangle. As you can see in the sketch below this is the case.
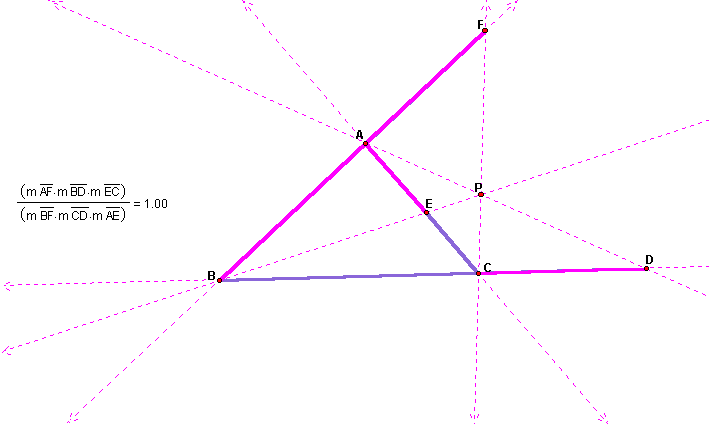
To explore this further click here to view a Geometer's Sketchpad Sketch of the above. Move P around and observe the results.
When P is anywhere inside triangle ABC, the ratio
of the areas of triangle ABC and triangle DEF is always greater than 4.
The ratio, however, is equal to 4 when P is at the centroid of the triangle
ABC. To explore this further click
here and remember to use the move button to move P to point G which
is the centroid of triangle ABC. This is the only time ratio of areas will
be 4. Now let us prove this point.
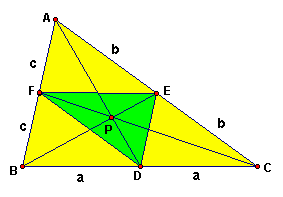
Point P is the centroid of the triangle ABC, and
thus the lines AD, BE, and CF are the medians of triangle ABC. We know
that BD = DC,
CE = EA, and AF = FB. For simplicity we will use
the following notations:
BD = DC = a or BC = 2a
CE = EA = b or AC = 2b
AF = FB = c or AB = 2c
Further, based on the Triangle Mid-segment Theorem we know that: In any triangle, a segment joining the midpoints of any two sides will be parallel to the third side and half its length. Thus,
EF = a
DE = c
DF = b
In order to find the area of triangle DEF we will use Heron's formula, which states that:
![]()
Where
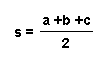
Now, to find the area of triangle ABC we need to work on the semi-perimeter of triangle ABC
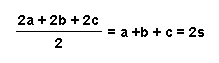
Using Heron's formula for area of triangle ABC would yield:
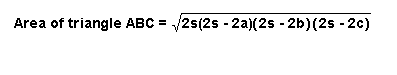
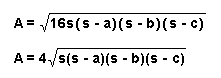
Or
Area of Triangle ABC = 4 * Area of triangle DEF
Based on the above, it can be concluded that when
P is at the centroid of triangle ABC the area of triangle ABC is four times
the area of triangle DEF.