These are a few special circumstances that I found while moving
point C around. Note that the dotted line segments of the equilateral
triangles have been hidden.
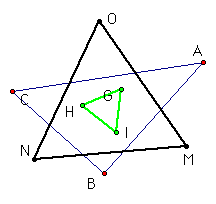 This first case is when the original 1st Napolean Triangle
has become the 2nd Napolean Triangle.
This first case is when the original 1st Napolean Triangle
has become the 2nd Napolean Triangle.
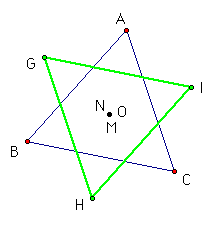 This shows when the three points of the 2nd Napolean
triangle converge to one point. Notice that triangles ABC and
GHI appear to be congruent. They are in fact congruent and the
single point made from N, M, and O, happens to be the circumcenter,
centroid, incenter, and orthocenter for both triangles.
This shows when the three points of the 2nd Napolean
triangle converge to one point. Notice that triangles ABC and
GHI appear to be congruent. They are in fact congruent and the
single point made from N, M, and O, happens to be the circumcenter,
centroid, incenter, and orthocenter for both triangles.
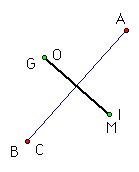 This shows when point C is on top of B. The same holds
for when C is on A.
This shows when point C is on top of B. The same holds
for when C is on A.
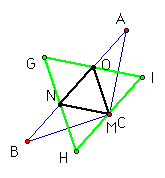 This shows when C is at point M. We have formed 4 congruent
triangles with the two Napolean Triangles. Triangles GNO, IOM,
HMN, and NMO are all congruent. Also, triangle AOC is congruent
to triangle BNC.
This shows when C is at point M. We have formed 4 congruent
triangles with the two Napolean Triangles. Triangles GNO, IOM,
HMN, and NMO are all congruent. Also, triangle AOC is congruent
to triangle BNC.
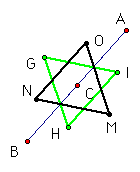 This shows when point C is at the midpoint of segment
AB. It appears, and is in fact true, that in this case, the two
Napolean triangles are congruent.
There are many more interesting findings, try to find
as many as you can.
This shows when point C is at the midpoint of segment
AB. It appears, and is in fact true, that in this case, the two
Napolean triangles are congruent.
There are many more interesting findings, try to find
as many as you can.
Return





