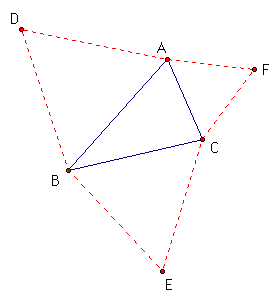
A Napolean Triangle is formed by choosing any given triangle. You then construct three equilateral triangles off each side of the given triangle as seen below:

Now, you find the circumcenter of each of the three equilateral triangles that you constructed. When you connect the three circumcenters, you will have a triangle known as the 1st Napolean Triangle. A picture is below:
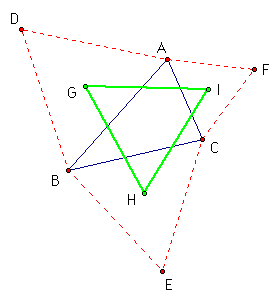
In the above picture, Triangle GHI is the 1st Napolean Triangle.
Now, there several interesting findings concerning the 1st Napolean Triangle. The first is that the 1st Napolean Triangle is actually equilateral. The proof of this is provided.
Another thing to mention is that there are actually two Napolean's Triangles. In the above picture, the equilateral triangles were constructed laying outside the original triangle. If the triangles are constructed so that they "lie on top" of the original triangle, the other, the 2nd Napolean's Triangle is formed.
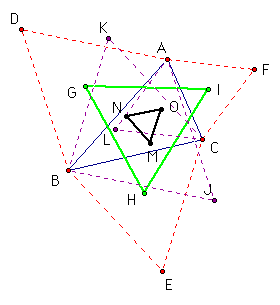
In the above figure, triangle MNO is the 2nd Napolean Triangle. When the points of the original triangle are moved, the two Napolean Triangles also change and can even change places. Try this for yourself. Because it does not matter which point you move, move point C. Try to find some interesting circumstances as you move point C around. After you try for a while, have a look at some special situations that I found.
Another interesting thing is that the two Napolean Triangles share the same centroid, circumcenter, orthocenter, and incenter.
The most interesting thing that I found deals with the relationship between the areas of the two Napolean Triangles and the area of the original triangle. It turns out that the difference in the areas of the two Napolean Triangles is equal to the area of the original triangle. Check out this phenomenon. Try this with each of the special cases mentioned above and see if this conjecture of mine holds for any situation.