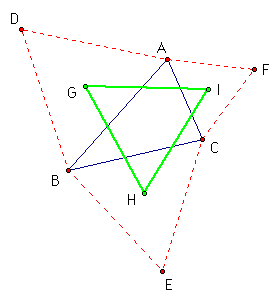
The following is a proof that Napolean's Triangles are equilateral.
Start with a given trianlge, ABC, the three equilateral triangles, ABD, BCE, and CAF, and the Napolean Triangle, GHI, constructed already.

Next, rotate the objects above twice, 120 degrees each time, with the point of rotation being point I.
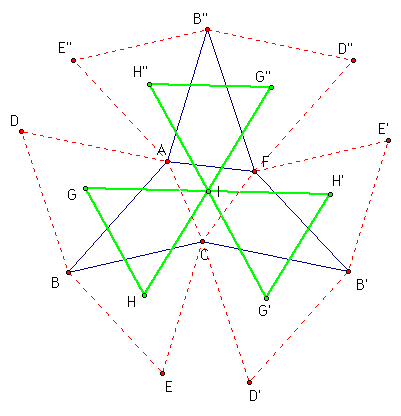
Because of the rotation, angles HIH', H'IH", and H"IH are all congruent and the measures of these angles is 120 degrees. Also by rotation, segments IH, IH', and IH" are congruent. Also, segments IG, IG', and IG" are congruent by rotation. Construct segments HH', H'H", and H"H. Label the intersection of HH' and IG' as J, the intersection of H'H" and IG" as K, and the intersection of H"H and IG as L.
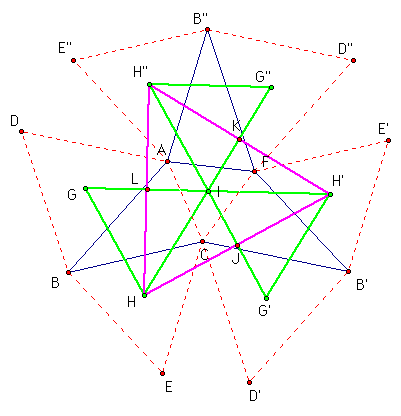
Now, because IH, IH', and IH" are congruent, triangles HIH, H'IH", and H"IH are isosceles (they are all congruent as well, but that is not needed for this proof). Because these triangles are isosceles, the angles opposite the congruent sides are congruent and because the total measure of the interior angles of a triangle must be 180 degrees, these angles must be 30 degrees. So, angles IHH', IH'H, IH'H", IH"H', IH"H, and IHH" are congruent and all have a measure of 30 degrees.
This leads us to say that, in particular, angles HJH", H'KH, and H"LH' are all 90 degrees.
This also shows that angles HIG', H'IG', H'IG", H"IG", H"IG, and GIH are all 60 degrees.
Construct segments HG', H'G", and H"G.
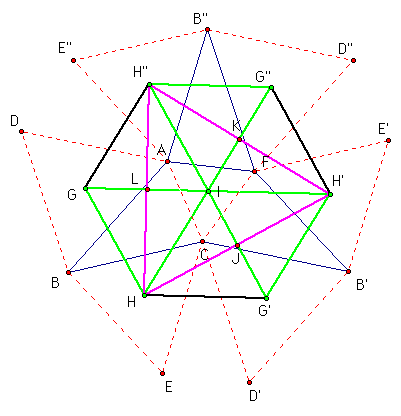
The figure GHG'H'G"H" is a regular hexagon because all interior angle measures are 60 degrees. Therefore, segments HG', H'G", and H"G are congruent to each other as well as congruent to GH, G'H', and G"H".
Construct GG'.
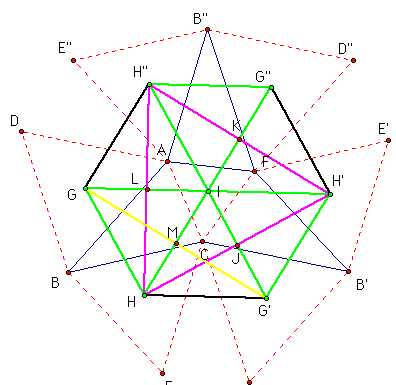
Because IG is congruent to IG', triangle GIG' is isosceles and angles IGG' and IG'G are congruent. We can also say that their angle measures are both 30 degrees.
Also, triangle GHG' is isosceles with angles HGG' and HG'G are congruent. Because H is one vertex of the aforementioned regular polygon, the angle GHG' must have degree measure of 120 degrees. This same argument holds for triangle H"GH with the vertex G and, in particular, angle H"GH.
By angle addition, angle IGH has an angle measure of 60 degrees, angle IHG likewise has angle measure of 60 degrees, and we have already shown that angle GIH has angle measure of 60 degrees. Therefore, triangle GHI is equiangular.
As a direct result, triangle GHI is also equilateral.