Objectives:
1) Learn to identify functions
2) Learn how to evaluate functions
3) Learn how to graph linear functions
1) Before we discuss how to identify functions, let's discuss what is defined to be a relation. A relation, in a mathematical sense, is defined to be any set of ordered pairs. What does this mean? Suppose we had two different equations that yielded the following table of values:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The first thing to note about each of these is that both are relations. Both fit the defintion that each input has an output, or in other words, each x value has a corresponding y value. Now, the important thing to note is that one of the two relations above is not a function and one of them is a function. This is the first way to identify functions. Look at each x value in the first table. Each x value has a unique y value that corresponds to it. No x value shares a y value. Now look in the second table. Does each x value have a unique y value that corresponds with it? No because when x is 1, y is 3 and when x is 3, y is also 3. So which one is a function and which is not? The relation represented by the first table is a function and the relation represented by the second table is not a function. So, if each x value has a unique corresponding y value, then the relation is a function.
The next way to determine if relation is a function is to do the vertical line test. After you have graphed a relation, you can use the vertical line test to determine if the relation is a function. If you can place a vertical line anywhere on the graph and the vertical line crosses the graph in two or more places, then the relation is not a graph. If there is no place on the graph that a vertical line will cross the graph in 2 or more places, then the relation is function. For example, look at the graphs below and determine, using the vertical line test, if the graph is that of a function or not.

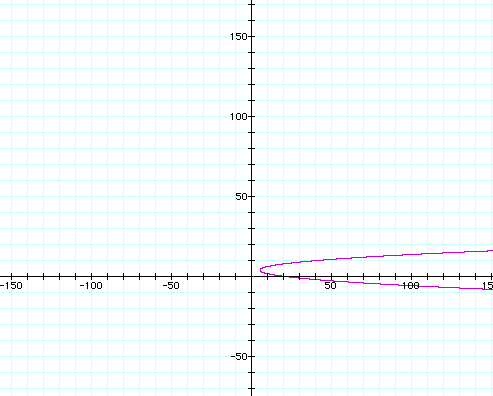
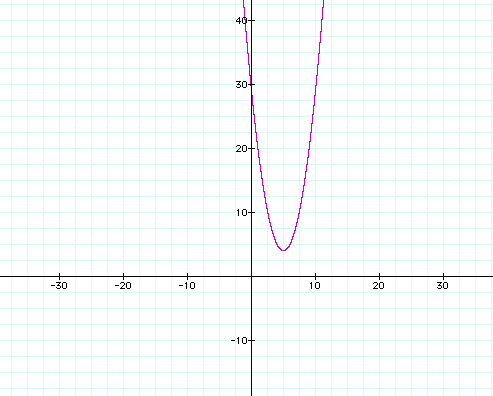
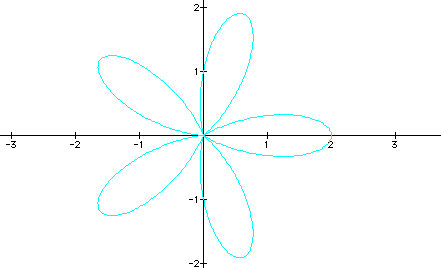
In the first and third graphs we see functions. In the second and fourth graphs, we see relations that are not functions because neither of these two would pass the vertical line test.
2) Evaluating functions is very similar to something done previously in this unit. On day 2, we learned how to verify solutions. We did this by substituting in values for x and y and looking to see if, in fact, that ordered pair was a solution. We also did a very similar thing that day when we derived our table of values that then allowed us to graph the equation. The one thing that is different about this is that instead of having, for instance, y=3x+12, we will have f(x) = 3x + 12. This is known as function notation. In reality, f(x) and y can be interchanged, but the f(x) helps you see that what y, or f(x), will be depends on what x will be. It lets us see that y varies according to x. So when given something like f(x) = 2x - 3 and asked to evaluate the function for a given value of the variable, then it becomes a subtitute and solve problem. For example, evaluate the given function, f(x) = 2x - 3 for x = 2; x = 4; and x = 5. This is really three problems but you do them the same way. For when x = 2, you substitute 2 in for x and you will have the following:
So, when x is 2, y, or f(x) is 1. The way to read the above answer is this: when the function is evaluated for x equal to 2, the result is 1.
Here are the answers for x = 4 and x = 5.
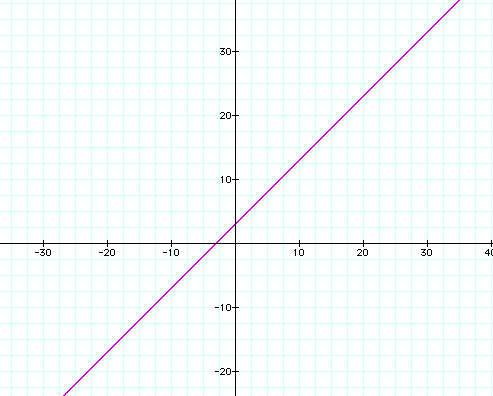
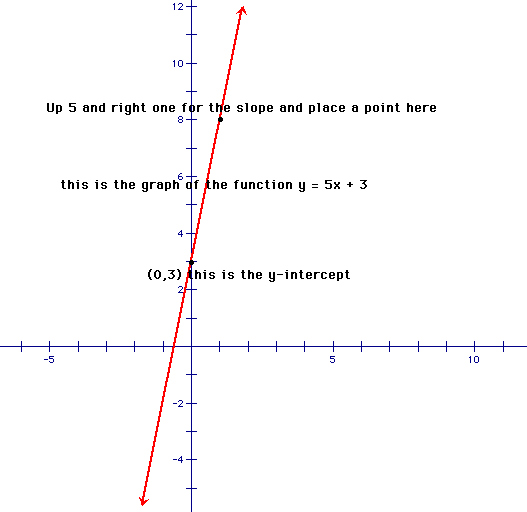
3) When graphing a linear function, you follow the same steps as we used in day 6. First rewrite the function into slope-intercept form. Then plot the y-intercept and use the slope to find the second point and then complete the graph by drawing a line through those two points. If I was wanting to graph the function, f(x)=3+5x, I would do the following. First rewrite this in slope intercept form. So, I now have y = 5x + 3. Now, I plot my first point at (0,3), the y-intercept and then go up 5 and then right 1, for my slope of 5, and make my second point there. I then draw a line through those points, and I have my graph. Your graph of this function should look like the one below.
Return to Instructional Unit overview