Objectives:
1) To learn the slope-intercept form of a line and be able to write the equation of a line in slope-intercept form, and to be able to identify what the slope and y-intercept are for a given equation
2) To be able to graph an equation written in slope-intercept form
3) To learn what makes two lines parallel
4) To be able to apply this knowledge to other situations
1) The slope intercept form of a line has two main components: the slope and the y-intercept. Both of these two topics have already been discussed in this unit before now. The general equation of a line written in slope intercept form is y = mx + b where m is the slope and b is the y-intercept. Give the students some examples where they are given the slope and the y-intercept and they have to write the equation of the line that has these two qualities. For example: If the slope of a given line is 3, m = 3, and the y-intercept is 4, b = 4, then what would the equation of the line be written in slope-intercept form? y = 3x + 4. Other examples could be given. Now, give them some examples where they have to write the equation in slope-intercept form and identify the two main components. For example: Identify the slope and the y-intercept in the following equations
a. y = 4x + 5
b. 3x = y - 7
c. 2y = 6x - 12
In a, the slope is 4, the y-int. is 5; in b, the slope is 3, the y-int. is 7, and in c, the slope is 3, the y-int. is -6. Other examples like these would be useful.
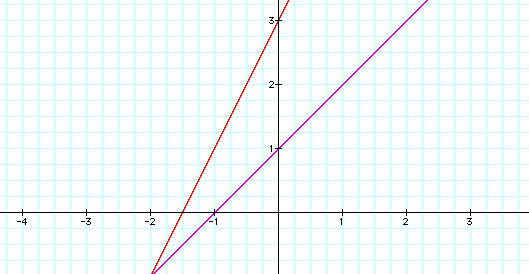
2) To allow the students to graph and understand what happens when the slope, y-int., or both changes, I would begin by using the graphing calculators or some other graphing software like the one shown below, Graphing Calculator 3.2.

In this case, my two equations were,
By using these two equations, I could vary what the slope, the y-int., or both were and therefore, allow the students to get a visual of what happens when they do change. Once the students worked with this for a little while, I would then have them do this by hand on graph paper. To explain this is quite easy, however, the students don't always get the idea so easily. The key is to plot the y-intercept first. If the students understand the y-intercept as having an ordered pair assosciated with it, as I tried to emphasize in an earlier lesson, then this should be easier for the students. After they plot the y-intercept, then they use the slope to find a second point. Say the y-int. 1 as in the second equation above. Then after plotting the y-int. go up one and over to the right one and make another point. Because the slope is 1, the rise over the run must be rise 1 and run 1. Because this was explained in further detail in a previous lesson, the students understanding should be okay for this topic. Give the students several chances at graphing. You could use the equations from part one above or make up other examples.
3) Before just telling the students what makes two lines parallel, pose this topic as a question and allow for some discussion. The students will provide some great insights and some terrible misconceptions as well. Filter through the responses with the students and allow them to decide among themselves what makes two lines parallel. The reason that many will give is that two lines are parallel because they never cross. Well, what about the two lines ensures that the lines will never intersect? Two lines are parallel because they have equal slopes. Again, this is a great time to use some graphing software to explore this topic. In the example given above in part two, a teacher could make m and k be equal and change b and c around and discuss what happens. There are many opportunities that arise here to explore some math technology.
4) Give the students a problem for which they can use the knowledge they just obtained. A great type of problem that I like is the following:
You and a friend are hiking some snow covered mountain trails in the Rocky Mountains. It is January 3rd and the temperature at the start of your hike was 40 degrees Fahrenheit. A severe cold front has hit and the temperature is going to drop 3.5 degrees every hour for the next 15 hours. You start your hike at 9:00 a.m. You have enough warm clothing so that you can be comfortable at a temperature of 12 degrees Fahrenheit. What time should you be back from your hike? What time do you need to turn around? How cold will it be at 10 p.m.?
To answer this, have the students derive an equation that models the data. This is a great opportunity to reinforce slope being a rate of change. The equation would be y = (-3.5)x + 40. The temperature is dropping 3.5 degrees every hour therefore, the slope is -3.5, and the initial temperature is 40 degrees and this is the y-intercept. Have the students graph the line with time being along the x-axis and temperature being on the y-axis. The graph should look something like the following:
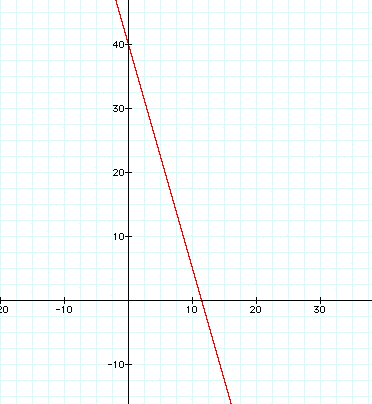
To answer what time you should be back, you could just look at the graph, find where the temperature is 12 degrees and see how many hours that corresponds with. With the graph that I presented above, it is hard to tell exactly how many hours corresponds to 12 degrees ( I provided this graph to save space) but it turns out that the corresponding hours is 8 hours. Does that mean that the two hikers has to be back at 8 p.m.? No, they must be back 8 hours after they started. So, they must be back at 5 p.m. What time do the hikers need to turn around and start back? Well they need to turn around after 4 hours of hiking. This will ensure that they make it back in 4 hours for a total of 8 hours of hiking. So, they need to turn around at 1 p.m. Now, how cold will it be at 10 p.m.? How many hours is that after 9 a.m.? You cannot just simply look at 10 hours along the x-axis. At 10 p.m., the temperature has been dropping for 13 hours. So looking along the x-axis, find 13 and see what the corresponding temperature would be. The temperature at 10 p.m. would be 5.5 degrees below 0 or -5.5 degrees Fahrenheit.
This problem can be revised a number of different ways. Take the basics and change whatever you like to fit your needs and the needs of your classroom.
Return to Instructional Unit overview