

Substance y = ax for![]()
Then
![]()
![]()
When x=0 the equations is conclusion with y=0. Therefore, if a is any number, there is the intersection of origin.
When x not = 0 then ![]()
If ![]()
![]()
therefore a=1
Then ,substance a=1 for ![]()
Then 0=3
It's not true. Therefore, as a=1, there is only intersection of origin.
If a not =1
![]()
![]()
And
![]()
The coordinates of the intersections without the origin are below.
![]()
The only sings differ from the two coordinates, so these two points are the central symmetry with the central point of origin.
For these coordination numbers are the real number:
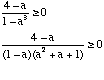
By the way
![]()
Therefore
For
![]()
![]() and
and ![]() so
so ![]()
or
![]() and
and ![]() so
so ![]()
Summary
As ![]() , there is the only intersection
of the origin.
, there is the only intersection
of the origin.
As ![]() or
or ![]() ,there
are three intersections.
,there
are three intersections.
![]() The intersections are
The intersections are
The two intersections of the first are the central symmetry with the center point of (0,0).