The
Parabola
The Northern Cross Radiotelescope
http://www.ira.cnr.it/Medicinaweb/Nc/DESCRIPTION.htm
|
The parabola is defined in
analytic geometry as the set of all points P in a plane that are
the same distance from a given line and a fixed point not on a line. The fixed point is called the focus and the
fixed line is called the directrix. |
Click here for
demonstration of the definition
Activity
A fun classroom
activity involving parabolas is paper folding with wax paper. The idea was
obtained from an article by Scott Smith
titled Paper Folding and Conic Sections.
Instructions
On the sheet of
wax paper draw a fixed line and a fixed point.
Fold the fixed point onto any point on the fixed line and crease the
paper. Repeat this many times. The creases form tangents to and envelope a
parabola. The
following is a GSP simulation of what takes place with the paper folding.
This exercise
leads to a nice presentation of the derivation of the standard equation of a
parabola whose vertex is at the origin.
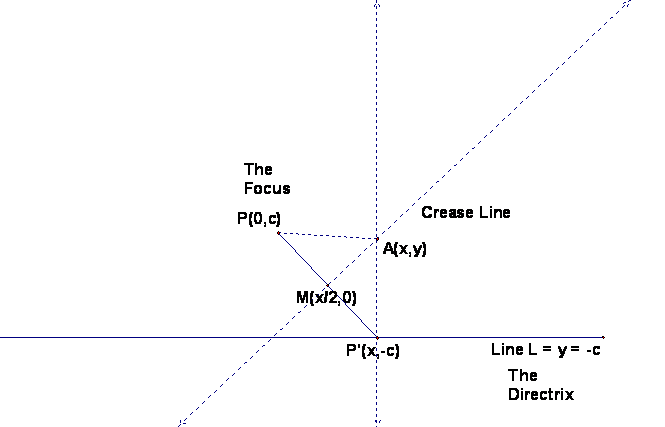
The figure below
shows point P called the Focus as the point that is
folded onto point P’ (located on The Directrix). At P’ a perpendicular line to the Directrix was constructed. This perpendicular line hits the
crease line at point A.
The crease line is the perpendicular bisector of PP’, thus point A
is equidistant from fixed point A and fixed the fixed line. Point A is a point on the parabola whose
focus is P and whose directrix is L.
(this can be proved by showing that the
crease line through A is tangent to
the parabola).
By definition of
a parabola the distance from point A to P is equal to the
distance from A to P’.
Recalling the distance formula
we can write the following
the
length of 
= the length of 
= 
or
by squaring both sides and multiplying out
or
the
standard form of an up/down parabola whose vertex is at the origin
The following activity was obtained from
Virginia Laird,
Students should
be provided with the below information through direct teaching and then
complete the following problems.
• The standard form of a parabola
with vertex 
is 
and
.
• A parabola is the set of all
points P in a plane that are the same distance from a given line and a
fixed point not on the line.
• The fixed point is called the
focus and the fixed line is called the directrix.
• The focus and the directrix are each located c units from the vertex,
but lie on opposite sides of the parabola.
• The parabola cannot intersect the directrix.
• The width of the parabola at its
focus is 4c units and is called the latus
rectum.
• A parabola’s direction is
dependent upon which term is squared in the standard form.
After the above
information has been given to the students they should be grouped in
pairs. They should then explore the
effects of (h,k) and c upon the parabola in
each of the
forms.
Graph the
following parabolas on the computer graphics program and draw conclusions about
the direction of the curve, the effect of (h,k) and c. Find the length of the latus
rectum for each curve and verify from the graph. Sketch the graph of each on your graph
paper. Also multiply each of the
equations out and solve for x or y accordingly.
1. 
2. 
3. 
4. 
Based on the
work that you have done above complete the following paragraph to enable you to
make some conjectures about parabolas.
|
A parabola in the form
of (x-h)^2=4c(y-k) turns
__________ or __________. When 4c is a negative number, the parabola turns __________, but
if 4c is positive, the parabola
turns __________. (h,k) represents the __________ of the
parabola. A parabola in the form
of (y-k)^2=4c(x-h) turns
__________ or __________. If 4c is positive the parabola turns
__________, but if 4c is negative the parabola turns
__________. The focus is
located__________ units from the vertex and the latus
rectum is __________
times this distance. |
Describe in
paragraph form the following parabolas.
Check your results by graphing each parabola on the computer.
1. 
2. 
Put the following
equations in standard form. Use above
conjectures to construct each parabola on graph paper
and use Graphing Calculator to verify graph.
1. 
2. 