Assignment 11: Polar Equations

by

Mike Cotton

This assignment is an investigation of polar equations. The polar equation that will be investigated is r = b cos (kθ).
The polar coordinates for a point P is written as the ordered pair (r, θ), where r is the distance from the origin, and θ is the angle in radians measured counter clock-wise from the horizontal axis. See Figure 1 below.

Figure 1

Part I

Lets take a look at the equation r = b cos (kθ). In this equation r is a function of theta.

Let k = 2, and let θ range from 0 to 2π. See Figure 2 below.
This graph was created by Graphing Calculator 3.2.
Figure 2
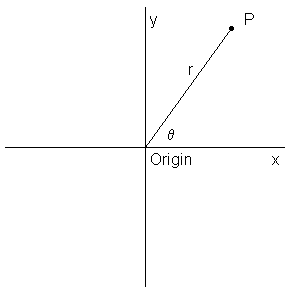
The curve above is called a four-leaved rose. In this example the number of leaves is twice the value of k. Note that as b increases the size of the "roses" increases. This can also be seen in the table below. 

Table 1
θ r b = 1 b = 2 b = 3 b = 4
0 1.0000 1.0000 2.0000 3.0000 4.0000
π/8 0.7071 0.7071 1.4142 2.1213 2.8284
π/4 0.0000 0.0000 0.0000 0.0000 0.0000
3π/8 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
π/2 -1.0000 -1.0000 -2.0000 -3.0000 -4.0000
5π/8 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
3π/4 0.0000 0.0000 0.0000 0.0000 0.0000
7π/8 0.7071 0.7071 1.4142 2.1213 2.8284
π 1.0000 1.0000 2.0000 3.0000 4.0000
9π/8 0.7071 0.7071 1.4142 2.1213 2.8284
5π/4 0.0000 0.0000 0.0000 0.0000 0.0000
11π/8 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
3π/2 -1.0000 -1.0000 -2.0000 -3.0000 -4.0000
13π/8 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
7π/4 0.0000 0.0000 0.0000 0.0000 0.0000
15π/8 0.7071 0.7071 1.4142 2.1213 2.8284
2π 1.0000 1.0000 2.0000 3.0000 4.0000

If you look at the row for θ = π, as b increases across the row, the value for r increases. You will also notice some negative values for r. See Figure 3 below.


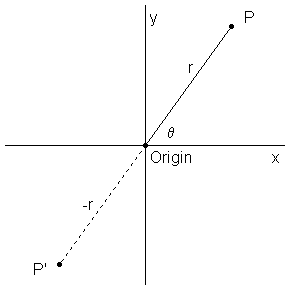
Figure 3

In the figure above P' represents a point with angle θ and a negative r.
Part II

Now lets take a look at the equation r = b cos (kθ) again, but let k = 3, and let θ range from 0 to 2π. See Figure 4 below.

This graph was created by Graphing Calculator 3.2.
Figure 4

The curve above is called a three-leaved rose. In this example the number of leaves is the value of k, and not twice k as in the previous example. Why? This can explained by the table below.


θ r b = 1 b = 2 b = 3 b = 4
0 1.0000 1.0000 2.0000 3.0000 4.0000
π/12 0.7071 0.7071 1.4142 2.1213 2.8284
π/6 0.0000 0.0000 0.0000 0.0000 0.0000
π/4 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
π/3 -1.0000 -1.0000 -2.0000 -3.0000 -4.0000
5π/12 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
π/2 0.0000 0.0000 0.0000 0.0000 0.0000
7π/12 0.7071 0.7071 1.4142 2.1213 2.8284
2π/3 1.0000 1.0000 2.0000 3.0000 4.0000
3π/4 0.7071 0.7071 1.4142 2.1213 2.8284
5π/6 0.0000 0.0000 0.0000 0.0000 0.0000
11π/12 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
π -1.0000 -1.0000 -2.0000 -3.0000 -4.0000
13π/12 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
7π/6 0.0000 0.0000 0.0000 0.0000 0.0000
5π/4 0.7071 0.7071 1.4142 2.1213 2.8284
4π/3 1.0000 1.0000 2.0000 3.0000 4.0000
17π/12 0.7071 0.7071 1.4142 2.1213 2.8284
3π/2 0.0000 0.0000 0.0000 0.0000 0.0000
19π/12 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
5π/3 -1.0000 -1.0000 -2.0000 -3.0000 -4.0000
7π/4 -0.7071 -0.7071 -1.4142 -2.1213 -2.8284
11π/6 0.0000 0.0000 0.0000 0.0000 0.0000
23π/12 0.7071 0.7071 1.4142 2.1213 2.8284
2π 1.0000 1.0000 2.0000 3.0000 4.0000
                                    Table 2


Let's take a look at the points for θ = 5π/12 [P = (-0.7071, 5π/12)] and θ = 17π/12 [P' = (0.7071, 17π/12)]. The figure below shows the two points on a graph.


Figure 5

As it turns out, the two polar coordinates above represent the same point. Polar coordinates differ from rectangular coordinates in that any point has more than one representation in polar coordinates. For example, the polar coordinates (r, θ) and (-r, θ + π) represent the same point P, as shown in Figure 5. More generally, this same point P has the polar coordinates (r, θ + nπ) for any even integer n, as well as (-r, θ + nπ) for any odd integer n. It becomes obvious that there are an infinite number of polar coordinates that can represent point P.

As it turns out the three-leaved rose in Figure 4 has created when θ reached π. For θ from π to 2π a second "rose" was created on top of the first one.

Assignment 10        Return to main Page        Assignment 12