

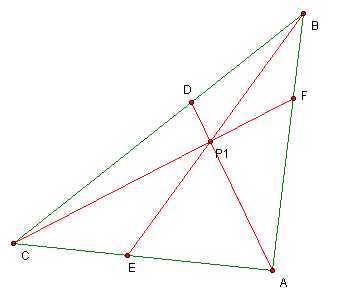
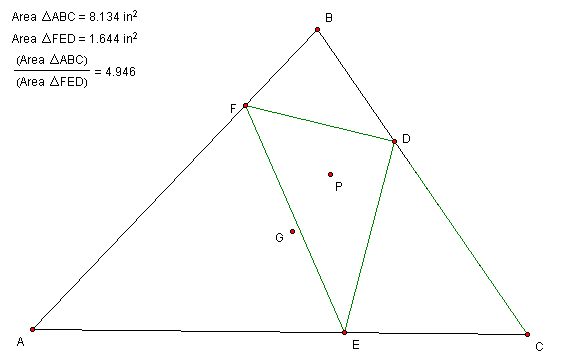
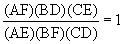 for allcases. Click Figure 2 below to try
moving point P yourself.
for allcases. Click Figure 2 below to try
moving point P yourself.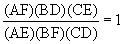 .
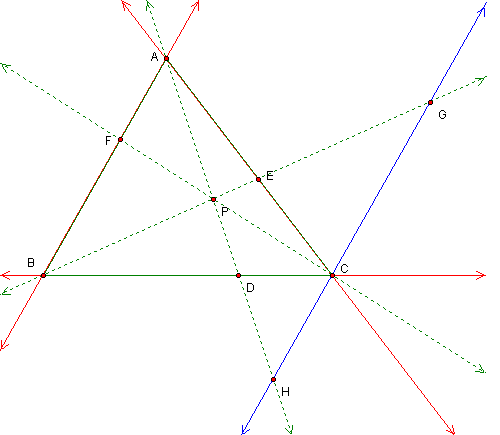
The segments BP, AP, & CP were extended and line HG was constructed
parallel to side AB and through point C. See figure 3 below. There are
several similar triangles,
.
The segments BP, AP, & CP were extended and line HG was constructed
parallel to side AB and through point C. See figure 3 below. There are
several similar triangles, 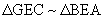 ,
, 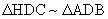 ,
, 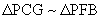 , &
, & 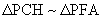 .
. 
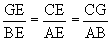 ,
, 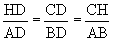 ,
, 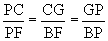 ,
&
,
& 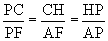 respectivly.
respectivly. 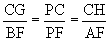 then
then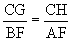 then
we finally get
then
we finally get .
. 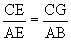 &
& 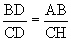 , and substitute into
, and substitute into 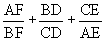 .
. 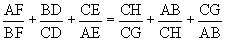 , where
, where 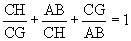 . So this proves
. So this proves 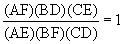
Assignment 12
Return
to main Page Student
Pages