The
Department of Mathematics Education
William Daly
EMAT6680
Write Up #6
Summer 03
Construction of a Triangle Given Arbitrary
Lengths of the Medial Triangle Sides
It should be clear that a triangle can be constructed from three line segments of arbitrary length. Call these segments j, k and l. If j, k and l are the lengths of the sides of a medial triangle, is it possible to construct the original triangle know only these lengths? The following demonstrates one method by which this can be accomplished.
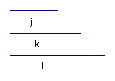
Start with three line segments of arbitrary length:
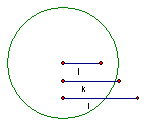
Consider first that if an endpoint of j and an endpoint of k are to be coincident, then the other endpoint of k must lie on a circle of radius k. Using GSP (Geometer Sketch Pad), this construction is illustrated by selecting the endpoint of j, selecting k, and then constructing a “circle by center + radius”:
Similarly, if the other endpoint of j and an endpoint of l are to be coincident, then the other endpoint of l must lie on a circle of radius l:
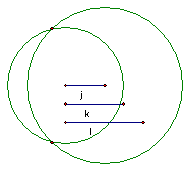
The intersection of these circles represents a point a distance k from the left endpoint of j and a distance l from the right endpoint of j. Connecting the intersection of the circles with the endpoint of j results in the medial triangle we are seeking. Before we proceed make a couple of observations. First there are actually two possible medial triangles. It should be apparent that one of these medial triangles is just the mirror image about segment j of the other, and that the triangle we are about to construct is also a mirror image about j. The mirror image is shown in dashed lines, which will be hidden from view in further sketches. A second observation is that the original arbitrary line k and l may be hidden from view; the radii of the two circles are equal length to k and l and are labeled as such:
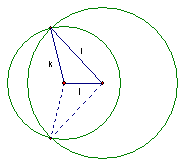
At this point in the discussion, we can speculate that the triangle to be constructed probably looks something like the sketch below::
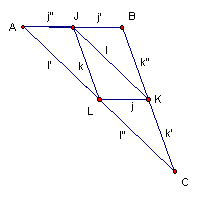
By definition of the medial triangle, the common endpoints of l’ and l” are a midpoint of the original triangle and an vertex L of the medial triangle formed by segments j and k. The same can be said of the common point between j’ and j” forming vertex J and also for the common point between k’ and k” forming vertex K. So the construction may be continued by asking whether there is a common point a distance l’ from point L and a distance j” from J. This point is found by noting that the j segment of the medial triangle twice the length of segment formed by j’ and j”. This fact, that the length of a side of the medial triangle is congruent to the segment on each side of the midpoint of the original triangle, is proven in Assignment 4. The construction then proceeds by centering a circle at L with radius l and another circle at J with a radius of j.
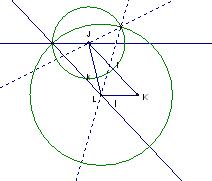
The resulting intersections are then both a distance l from L and a distance j from J. These intersections are connected by line which lies along the edge of the original triangle.
But what about the fact that there is a second set of intersections that meet the requirement of being distance j from J and l from L? These are connected with dotted lines. How do we know which one is the correct intersection? This becomes apparent from the next step in the construction where the common point at the intersection of j’ and k” is located. This is done again by constructing a circle of radius j centered at J (already done above) and constructing a new circle of radius k at K. In doing so, notice that the dotted line through J does not pass through the intersection of circles J and K, but the solid line does.
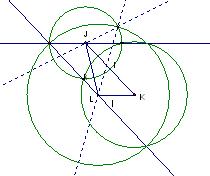
So it is this segment, AB that has at one endpoint a distance of l from L and a distance j from J. The other endpoint is a distance j from J and a distance k from K. This last statement is not true of the associated dotted line.
The final step in the construction is to consider a common point a distance k from K and a distance l from L. These points occur at the intersection of the two circles centered at K and L, with radii K and L respectively. These two circles are already drawn; it is now just a matter of connecting the intersections through the corresponding radii:
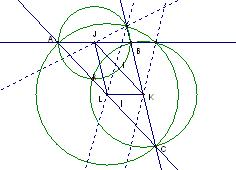
Again, there are two possible lines. As before, it is concluded that the dotted line does not meet the condition of having a common point a distance l from L and distance k from K. The solid line does meet this condition. In this last sketch the vertices of the assumed triangle, A, B and C are shown. The sketch is cleaned up below by hiding the dotted lines, and connecting ABC, and jkl in bold segments:
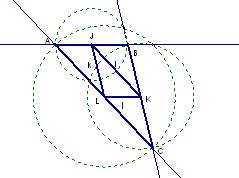
To summarize, the medial triangle from arbitrary segments jkl was constructed by centering circles of radius k at one endpoint of j and of radius l at the other endpoint of j. The medial triangle then drawn from the endpoints of j to the intersecting point on the circles. Turning our attention to the assumed original triangle, constructions are done by noting that a circle centered on a midpoint will have a diameter twice the opposite leg of the medial triangle. When this is done at each vertex of the medial triangle, which is by definition also the midpoint of the original triangle, the intersections of these circles are the vertices of the original triangle; but only the intersections that meet the condition of simultaneously being one half the length of the original triangles side to the corresponding midpoints.
