

Theorem:
The Area of a right triangle is given to be equal to 1/2 the product of its sides or legs
Given below is a right triangle ABC where angle CBA is a 90 degree angle. The segments CB and AB are
the sides or legs of the right triangle. The segment AC is the hypotneuse of the right triangle. It is the
segment opposite the 90 degree angle.
We want to show that the area of the right triangle
ABC is 1/2(AB)(BC). How do we do this?
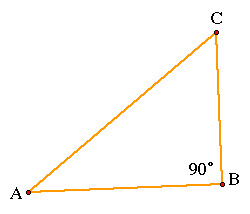
Here we go!
We can make a rectangle by using this triangle so that we get something that looks like the following:
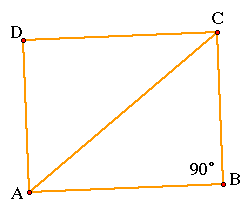
Now, we have a rectangle ABCD such that all four angles are 90 degrees,
not only angle CBA. Since ABCD is a rectangle, the line segment DC is
parallel to the segment AB and also the segment DA is parallel to the
segment CB. Hence, the segment AC is known as a transversal because it
cuts across a set of parallel lines or segments. Since segment AC is a
transversal and segments DC and AB are parallel lines, then we have
certain alternate interior angles that are congruent. They are shown below.
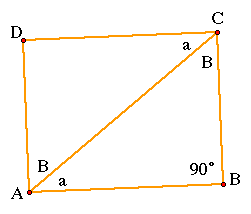
The angles a and a are alternate interior angles and therefore, are
congruent by the Alternate Interior Angles Theorem. Also, the angles B
and B are alternate interior angles and therefore, congruent by the
same reasoning. Therefore, the two triangles that make up the rectangle
ABCD are congruent by Angle-Side-Angle Congruence since they have two
congruent angles and an included side congruent (since AC is congruent to
itself). We can label the two congruent triangles as T1 and T2.
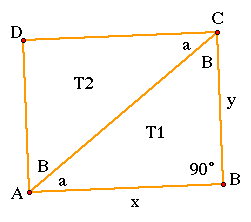
The area of the rectangle ABCD is equal to (x)(y) where x = AB
= base and
y = BC = height. Since T1 + T2 makes up the area of the whole rectangle
ABCD, we can set the two areas equal to one another.
So, (x)(y) = Area T1 + Area T2. Since we discovered that T1 and T2 are
congruent triangles by ASA (Angle-Side-Angle) Congruence, (x)(y) =
2(Area T1). Therefore, the Area T1 = 1/2(x)(y) = 1/2(AB)(BC).
Hence, we have shown that the area of a right triangle is equal to the product of its legs.
Well, isn't there a theorem that states that the Area of any triangle is equal to the product of its base multiplied by its height?
Area of a triangle = 1/2(base)(height)
There sure is: Let's try proving this using two different cases!
Case 1: Acute Triangle Case
(Additive Case)
When we have an acute triangle, we can prove the area of the triangle is 1/2(base)(height) as follows:
Given a triangle ABC where all the angles in ABC are acute angles and h is the perpendicular distance from the point B to the segment AC, we want to show the area of triangle ABC is 1/2(AC)(BD).
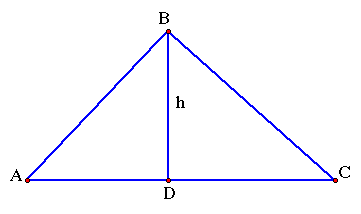
Since h is perpendicular to the segment AC, then angle BDC and angle BDA are both 90 degree angles. So, we can use what we know from the right triangle case to prove this case since triangle BDC and triangle BDA are both right triangles!
The area of triangle ABC = area of triangle ADB + area of triangle CDB. Using the illustration below, the area of triangle ABC = T1 + T2.
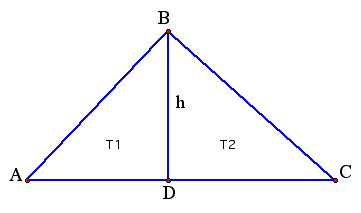
The area of T1 = 1/2(AD)(BD)
The area of T2 = 1/2(DC)(BD)
Area of triangle ABC = (1/2(DC)(BD) + 1/2(AD)(BD))
Factoring a 1/2 and (BD) out of both, we get
Area of triangle ABC = 1/2(BD)((DC)+(AD)). Since (DC)+(AD) = (AC), we
have proved the area of triangle ABC = 1/2(AC)(BD).
Case 2: Obtuse Triangle Case
(Subtractive Case)
When we have an obtuse triangle, we can prove the area of the triangle is 1/2(base)(height) as well:
Given an obtuse triangle ABC where h is the perpendicular distance from the point C to the segment AB, we want to show the area of triangle ABC is 1/2(AB)(CD). AB is considered to be the base and CD is the height.
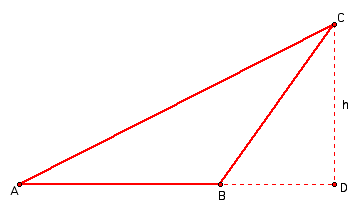
Angles CDB and CDA are the same 90 degree angle since h is the perpendicular distance from the point C to the segment AB. They make up two different right triangles. So, triangle CDB is a right triangle and triangle CDA is a right triangle.
The area of triangle ABC can be thought of as the area of triangle CDA minus the area of triangle CDB.
Area of triangle ABC = Area triangle CDA - Area triangle CDB
Area of triangle ABC = 1/2(AD)(CD) - 1/2(BD)(CD)
Factoring a 1/2 and (CD) out, we are left with
Area of triangle ABC = 1/2(CD)((AD)-((BD)).
Since (AD)-(BD) = (AB), the area of triangle ABC = 1/2(AB)(CD).
Thus, we have proved the area of a triangle equals its base times its height for all triangles!