

1. Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. Prove whatever you find.
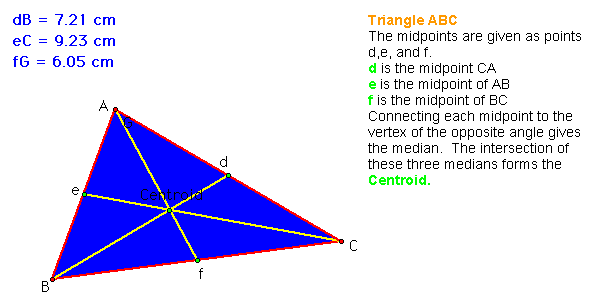
This is the original triangle ABC and its medians. The intersection of the medians as shown above forms the Centroid of the triangle.
Now, let's form a second triangle that has its three sides the lengths of the three medians of the first triangle. We then want to find a relationship between the two triangles.
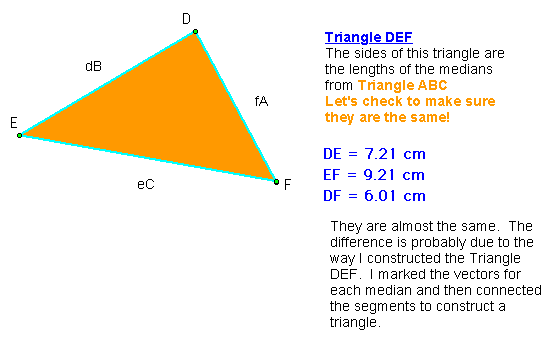
Now, let's compare the triangles to see if they are congruent or similar. I measured the side lengths, the median distances, the angles of the different triangles, the perimeter, and the area. See the insert done below in GSP for these calculations.
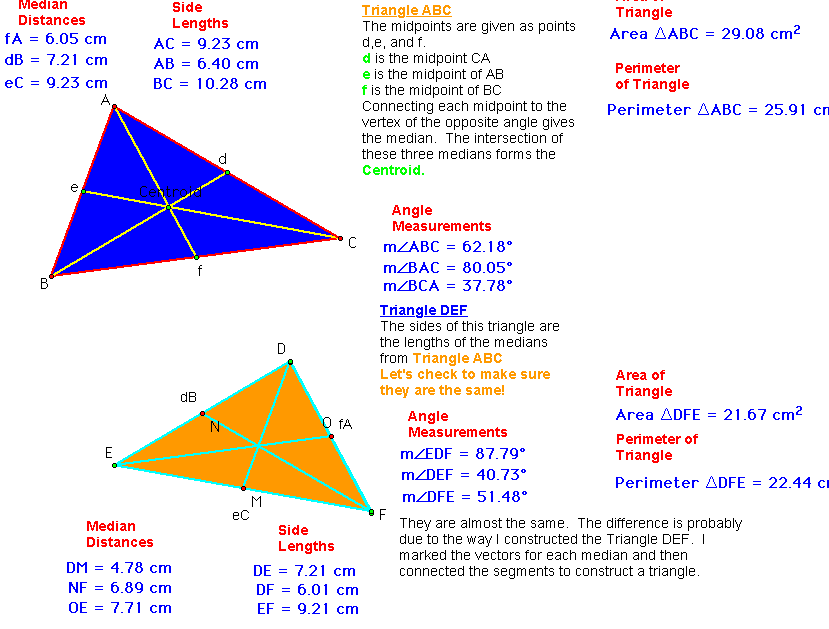
I didn't have any luck when comparing the length sides, the median lengths, the angles, the perimeter, the area, etc. I coudn't find any solid ratios that were consistent. I really couldn't find anything that was the same.
It would make sense that the perimeter of Triangle DEF would be less than the perimeter of Triangle ABC since the median lengths are smaller than the side lengths in Triangle ABC. This would, in turn cause the area to be different as well.
This concludes my investigation of the triangle and its medians.