Assignment 2: Parabola Investigation
by
Melissa Silverman
Continuing my thoughts from Assignment
1, it is important for students to isolate parts of equations
and manipulate them so that they can determine the role of that
component in the equation. For this assignment, I will explore
using the equation
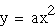
Before I begin manipulating the equation,
I will graph the equation when a=1 to begin my understanding of
the equation.
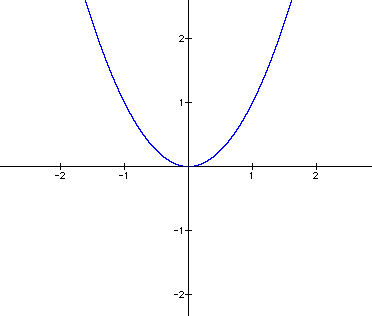 blue
blue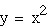
From my intial graph, I can see that
the basic form I am working with is a parabola. I can begin to
make a few hypotheses about parabolas from my initial graph. I
chose a to be a positive number and the parabola faces upwards.
What if a were negative? Would it point down? To test this hypothesis,
I can set a=-1.
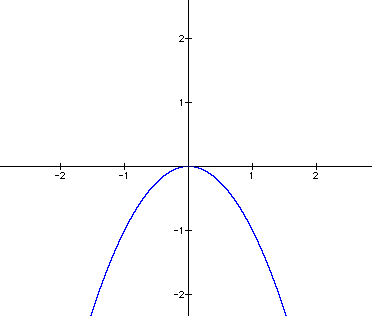
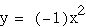 The vertex, or center point, of the
parabola has not changed. The curvature of the parabola has not
changed. The parabola now opens downward. So by experimenting
with the sign of the coefficient, one may conclude that a positive
coefficient will result in an upward facing parabola while a negative
coefficient will result in a downward facing parabola.
The vertex, or center point, of the
parabola has not changed. The curvature of the parabola has not
changed. The parabola now opens downward. So by experimenting
with the sign of the coefficient, one may conclude that a positive
coefficient will result in an upward facing parabola while a negative
coefficient will result in a downward facing parabola.
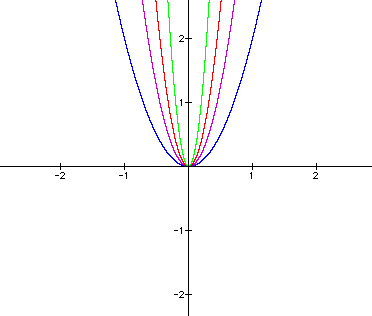
A conclusion has been drawn about the
parabola in regards to the sign of the coefficient. What about
the value of the coefficient? As the coefficient becomes larger
or smaller, how does that affect the shape of the parabola? By
plugging in various coefficient values and graphing them on the
same graph, I can draw some conclusions.
 blue
blue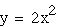 purple
purple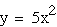 red
red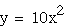 green
green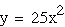 The center, or vertex, of the parabola
remains at the origin. All of the chosen coefficients are positive,
and all of the parabolas are facing upwards. The only difference
in the graphs is the width, so the conclusion can be made that
the larger the coefficient, the narrower the parabola. Inversely,
the smaller the coefficient, the wider the parabola.
The center, or vertex, of the parabola
remains at the origin. All of the chosen coefficients are positive,
and all of the parabolas are facing upwards. The only difference
in the graphs is the width, so the conclusion can be made that
the larger the coefficient, the narrower the parabola. Inversely,
the smaller the coefficient, the wider the parabola.
Neither the sign of the coefficient
nor the value of the coefficient change the parabola's center.
What if I want to move the parabola to the left or right? What
can I change to move the vertex along the x-axis? I will try adding
and subtracting a constant to x before I square the term.
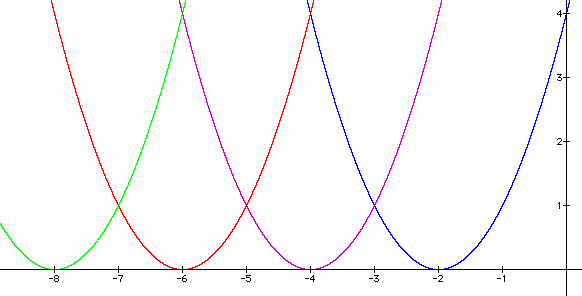
 blue
blue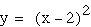 purple
purple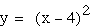 red
red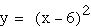 green
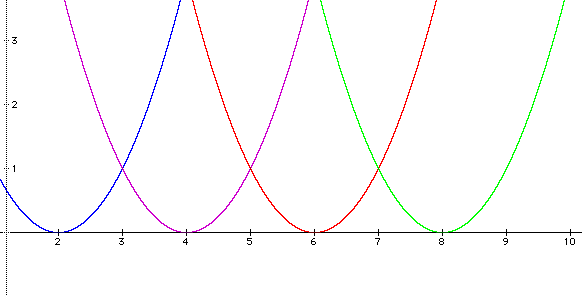
green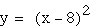 Subtracing a constant from the coefficient
(before squaring) moves the vertex along the positive x-axis.
The vertex's movement corresponds exactly to the value of the
constant. For example, the blue parabola has moved over 2 units,
and 2 is its constant. I can move the parabola's vertex to any
positive x value by subtracting that value from x. I can now infer
that adding a constant to the coefficient will move the vertex
along the negative x-axis.
Subtracing a constant from the coefficient
(before squaring) moves the vertex along the positive x-axis.
The vertex's movement corresponds exactly to the value of the
constant. For example, the blue parabola has moved over 2 units,
and 2 is its constant. I can move the parabola's vertex to any
positive x value by subtracting that value from x. I can now infer
that adding a constant to the coefficient will move the vertex
along the negative x-axis.
 blue
blue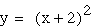 purple
purple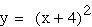 red
red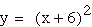 green
green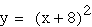 As predicted, adding a coefficient
moves the vertex along the negative x-axis. The vertex's movement
corresponds to the value of the constant.
As predicted, adding a coefficient
moves the vertex along the negative x-axis. The vertex's movement
corresponds to the value of the constant.
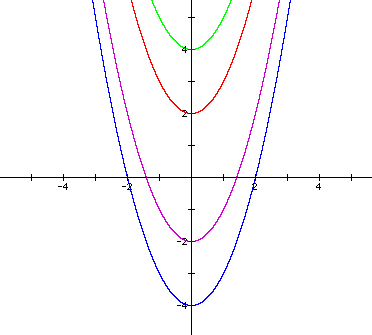
The last manipulation is moving the
parabola along the y-axis. To accomplish this, add or subtract
a coefficient after the squared term.
 blue
blue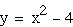 purple
purple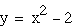 red
red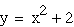 green
green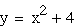 Adding or subtracting a constant after
the squared term lowers or raises the vertex along the y-axis,
respectively. Furthermore, the value that I add or subtract from
the parabola is the parabola's y-intercepts. Thus I can control
where the parabola crosses the y-axis.
Adding or subtracting a constant after
the squared term lowers or raises the vertex along the y-axis,
respectively. Furthermore, the value that I add or subtract from
the parabola is the parabola's y-intercepts. Thus I can control
where the parabola crosses the y-axis.
By graphing the equation
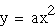 while manipulating it in different
ways, we have the ability to produce desired parabolas and make
predictions about the graphs of equations in this form. By changing
the coefficient and inserting coefficients in different combinations,
one can control the orientation, width, and vertex placement of
a parabola.
This activity fosters flexibility to
students in their understanding of parabolas. They can look at
parabolic equations and predict what the graph will look like.
They can also look at a parabola and create the corresponding
equation. Knowing how each part of the formula works means they
can take any graph or equation of a parabola and manipulate it
to meet their needs. Just as students need the flexibility to
think in decimals and fractions, students need to be able to think
of equations in terms of their graphs and graphs in terms of their
equations to reach higher mathematical understanding.
To continue my thoughts from the previous
exercise, this activity fosters curiosity and a list of questions.
I formatted my assignment the way a student might think. Beginning
with a simple parabola, what questions might I have about it?
My line of questioning focused on ways to get the parabola I wanted
by changing the formula. By focusing on things that I could change
about the graph, I discovered how to determine whether the parabola
faces up or down, how to move the vertex of the parabola, how
to affect the curvature of the parabola, and even how to determine
the y-intercept. By plotting several examples on one graph, I
not only determined what was being changed but how it was being
changed. More specifically, how does a coefficient or constant's
value affect the parabola? These are all logical steps that students
could follow and have much sucess with. Allowing students to discover
mathematics on their own is sometimes hard to accomplish. Technology
allows students to tinker and experiment, learning on their own
what would traditionally be presented through textbook pictures
and class notes.
while manipulating it in different
ways, we have the ability to produce desired parabolas and make
predictions about the graphs of equations in this form. By changing
the coefficient and inserting coefficients in different combinations,
one can control the orientation, width, and vertex placement of
a parabola.
This activity fosters flexibility to
students in their understanding of parabolas. They can look at
parabolic equations and predict what the graph will look like.
They can also look at a parabola and create the corresponding
equation. Knowing how each part of the formula works means they
can take any graph or equation of a parabola and manipulate it
to meet their needs. Just as students need the flexibility to
think in decimals and fractions, students need to be able to think
of equations in terms of their graphs and graphs in terms of their
equations to reach higher mathematical understanding.
To continue my thoughts from the previous
exercise, this activity fosters curiosity and a list of questions.
I formatted my assignment the way a student might think. Beginning
with a simple parabola, what questions might I have about it?
My line of questioning focused on ways to get the parabola I wanted
by changing the formula. By focusing on things that I could change
about the graph, I discovered how to determine whether the parabola
faces up or down, how to move the vertex of the parabola, how
to affect the curvature of the parabola, and even how to determine
the y-intercept. By plotting several examples on one graph, I
not only determined what was being changed but how it was being
changed. More specifically, how does a coefficient or constant's
value affect the parabola? These are all logical steps that students
could follow and have much sucess with. Allowing students to discover
mathematics on their own is sometimes hard to accomplish. Technology
allows students to tinker and experiment, learning on their own
what would traditionally be presented through textbook pictures
and class notes.
Assignment
1 | Home Page | Assignment
3





