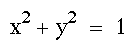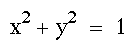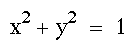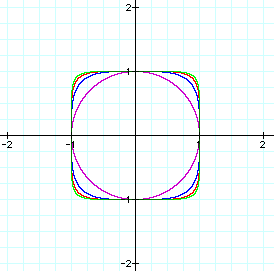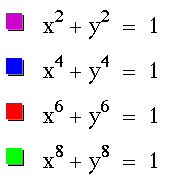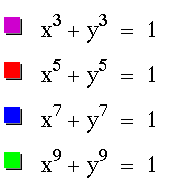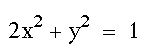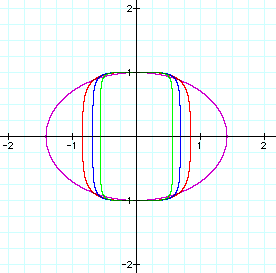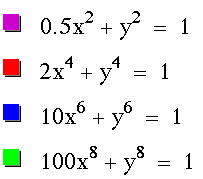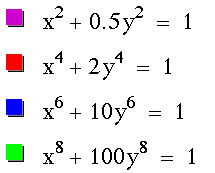Assignment 1: Exploring Graphs
by
Melissa Silverman
The equation
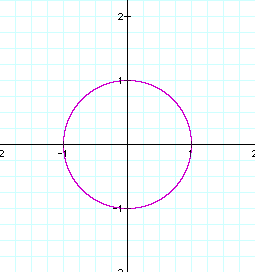
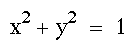 describes a circle with a radius of
1 and a center of (0,0).
describes a circle with a radius of
1 and a center of (0,0).
If x and y are raised to an even power, such as
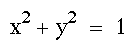 then the graph is an enclosed shape.
Notice that as x and y are raised to a higher (even) power, the
enclosed shape becomes more and more similar to a square. Like
the graph above, the square shape has a center of (0,0).
then the graph is an enclosed shape.
Notice that as x and y are raised to a higher (even) power, the
enclosed shape becomes more and more similar to a square. Like
the graph above, the square shape has a center of (0,0).
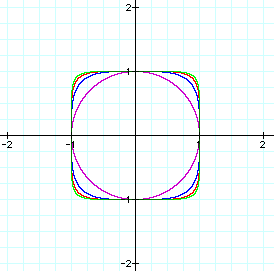
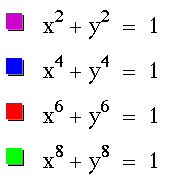
If x and y are raised to an odd power, such as
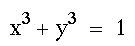 ,
then the graph has a similar square-like
quality around the origin and approaches the line y=-x as x and
y are increasing.
,
then the graph has a similar square-like
quality around the origin and approaches the line y=-x as x and
y are increasing.
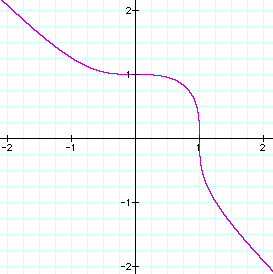
As x and y are raised to a higher odd
power, the graph gets closer and closer to a square corner around
the origin and approaches y=-x as the values of x and y increase.
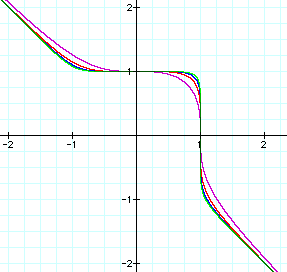
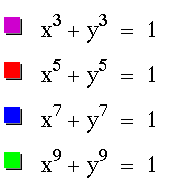
So if x and y are raised to an even power, then the graph will
be an enclosed shape, centered around the origin, that approaches
a square. As x and y become larger, the graph becomes more
and more square. If x and y are raised to an odd power, then the
graph will have a curved shape that approaches a corner about
the origin and approaches y=-x as x and y become larger.
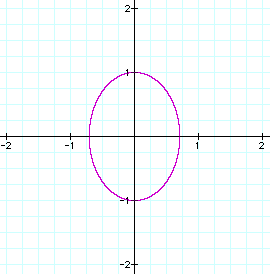
Suppose x has a coefficient, such as in
the equation
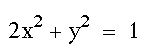 The width of the circle has decreased
to form an ellipse. The center of the ellipse remains at (0,0).
The height of the ellipse remains at 2 units.
The width of the circle has decreased
to form an ellipse. The center of the ellipse remains at (0,0).
The height of the ellipse remains at 2 units.
As the coefficient increases, the ellipse
becomes more rectangular, while the height and the center of the
shape are unaffected. Inversely, as the coefficient becomes smaller,
the ellipse broadens and becomes wider.
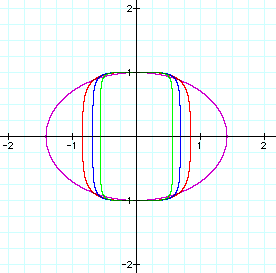
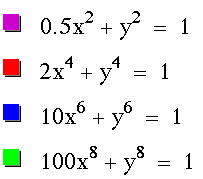
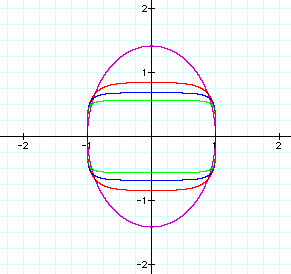
Changing the coefficient of y changes the height
of the enclosed figure. As the coefficient decreases, the shape
resembles an ellipse. As the coefficient increases, the figure
becomes more like a rectangle.
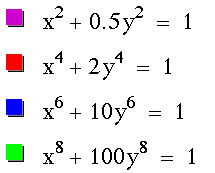
This investigation helps visualize the impact
made on a simple equation by altering the components of the equation.
By changing and isolating different components of an equation,
conclusions can be drawn about the functions of the components.
The graph of the equation takes on many forms, from enclosed figures
to large hyperbolas. By altering the equation's characteristics,
one can conclude upon the role of each part of the equation and
gain a deeper understanding of the equation.
In an educational setting, this process
can help students understand equations. By being able to change
equations and graph them instantly, students can see the impact
that their changes are making. Changing coefficients, exponents,
and other elements in an equation correspond to different characteristics
when graphed. Having control over those changes can help students
comprehend equations and their uses. In a classroom, students
could conduct a similar investigation to the one above. Once students
have learned the basic formula for a circle, they may be encouraged
to generate a list of questions. What happens when I add a coefficient
to the x or y term? How can I move the center of the circle so
it is not at the origin? What if the equation is equal to something
other than one? I think this sort of questioning, followed by
computer time to find answers to these questions, would be a great
educational experience for the students. Much like in science
class, they can ask questions, form hypotheses, and then test
them using technology. And because each student would be questioning
different things, the activity could be concluded by letting the
students share their discoveries with the class. This would encourage
mathematic communication and foster curiosity because students
would want to know what everyone else was discovering, in addition
to being eager to share their own findings.
This process could easily be applied
to all levels of mathematics. For early algebra students, this
same process of discovery could be applied to the equation of
a line or parabola. For advanced geometry students, this could
be conducted for any of the conic sections. Geometry students
can test area and volume formulas. This is a general educational
concept that can be applied sucessfully to many mathematical concepts.
Assignment
12 | Home Page | Assignment
2