Assignment 4: Investigating Triangles
by
Melissa Silverman
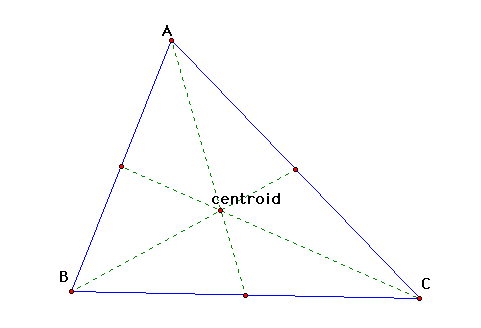
The centroid of a triangle is the point
of intersection for the three lines from each vertex to the midpoint
of the side opposite the vertex.
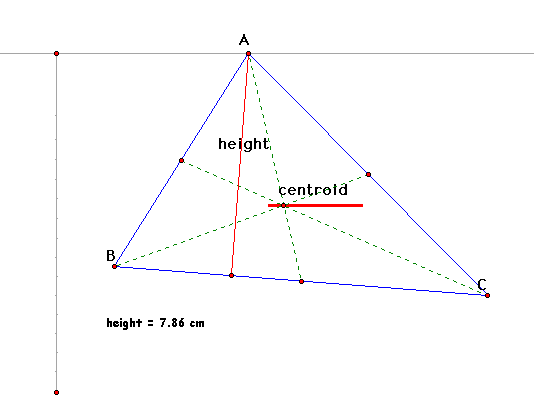
How is the centroid's position affected
by the shape of the triangle? Using the GSP trace tool, one can
change the triangle and track the movement of the centroid. In
this first construction, we are experimenting with moving only
one vertex, Point A, along a line. When Point A is moved along
the line, the centroid's path is also a straight line. Its path
is parallel to the line that Point A is being moved on. Notice
that the height of the triangle changes as Point A moves, but
the centroid continues to move along a straight path.
When one point of the triangle is moved
along a line, then the centroid follows along a straight line.
What happens if more than one point of the triangle is moved?
In the following construction, two points of the triangle are
moved along a line.
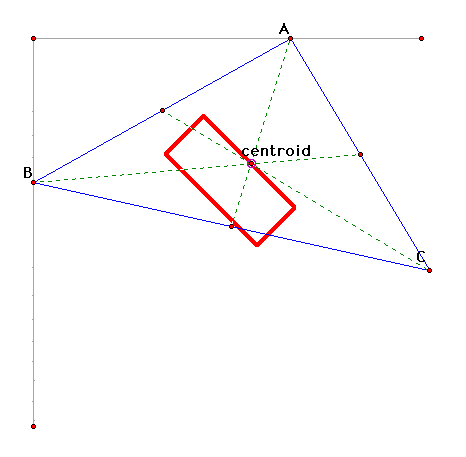The centroid moves along a rectangular
path. As points A and B move along the gray lines, the centroid
traces a rectangle. So when two points are moved along perpendicular
lines, the centroid follows a rectangular path. Similar to before,
the cetroid moves along an orderly path, as opposed to jumping
all over the construction.
What happens if all three points are
moved along a straight line?
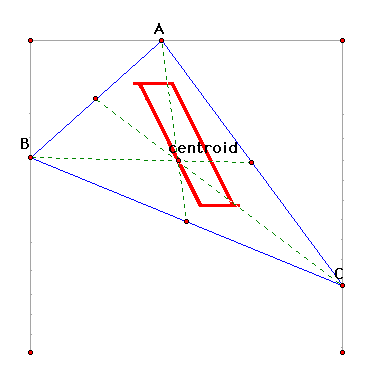The path of the centroid is a parallelogram.
Again, as points A, B, and C move back and forth along their lines,
the centroid follows a predictable path.
These past few examples only explore
what happens when the points travel along perpendicular lines.
What happens if the lines are constructed at an angle. Does the
centroid still follow a particular path?
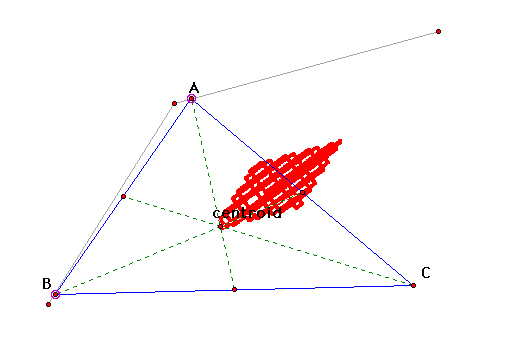The centroid follows along a lattice
in the shape of a parallelogram. The path is not as orderly as
when the lines are at right angles, but the path of the centroid
does trace a particular design composed of straight lines and
right angles.
What if the vertexes of the triangle
were moved around a circular path? Moving two of the three points
around the circle, while tracing the centroid, results in a path
that looks like a flower.
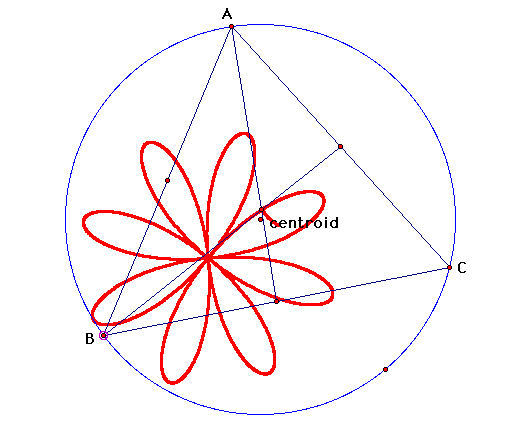
This exercise fostered a lot of
curiousity and excitement. As the constructions got more complex
and the centroid paths more interesting, peers began to peek over
and give their input. We had fun inventing new ways of moving
the triangle and predicting the effect that that movement would
have on the centroid's path. This exercise is visually enticing,
so it sparks interest and lots of communication between students.
I also like the fact that the constructions required
for this exercise are easy, but the results are impressive. Students
with little practice on GSP could complete this exercise. It is
a great way to break into GSP's capabilities, especially with
the animation tool.
I was also very impressed by the power
of the trace tool in the investigation. It is easy to make a triangle
and use a GSP tool to find the centroid. It is also easy to just
move around the vertices of the triangle and watch the centroid
wiggle. But when the centroid is traced and its path is drawn,
it really brings up some neat points. Prior to tracing the centroid,
I did not think much about where it was going as the triangle
around it changed. My hypothesis was that the centroid would not
follow an orderly path. But if the vertices of the triangle are
moved on a path, the cetroid draws a very clear path. Even after
changing the characteristics of the animations (speed, direction,
etc.), the centroid paths were controlled.
The only thing that bothers me about
this discovery is that I am not sure how much mathematics this
is supporting. It helps to understand the relationship between
the centroid and the triangle, but I am afraid I cannot see too
many educational applications of this discovery.
Assignment
3 | Home Page | Assignment
5