Investigation of Polar Equations
By: Denise Natasha Brewley and Venki Ramachandran
To begin our investigation, we consider polar equations of the following form, where a, b, n are integers such that a=b >0.
r = acos(nq) and r=a+bcos(nq)
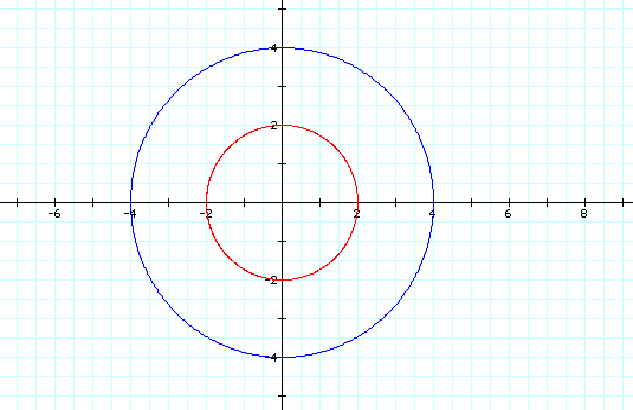
For this case we consider when a=2 and b=2. Notice that for this case, as depicted below, the graph of three polar equations are given including the equation of r=2. We will first consider what happens when n=0 and how this impacts our graphs. Notice that for the n=0 case, the equations r=2cos(nq) and r=2 are the same - they overlap. This follows because cos(nq)=cos(0)=1. We have a graph of two concentric circles such that the blue circle has radius 4. This also follows because r=2+2cos(nq) simplifies to r=2+2(1) = 4.
![]()
![]()
![]()
We now want to know what happens to our graphs when a and b are fixed but n varies.
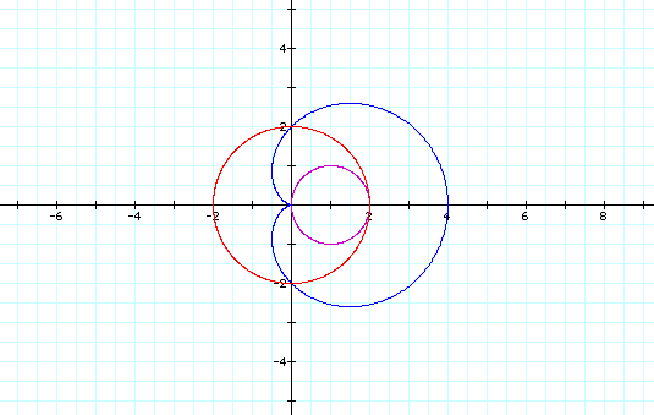
Now let us investigate the n=1 case. Notice that our purple graph becomes r=2cosq which is the graph of a circle. For q in the interval 0<q<2p, we can get a full range of values for r given below. As q increases from 0 to 2p, the values of r on our circle start at 2 for q=0 and ends at 2 for q=2p. This explains why the graph of r=2cosq is translated to the right two units as opposed to centered at the origin. Notice for this equation that the radius of this circle is 1. Lets figure our why this is so. We can conjecture that for r=acosq, a is the diameter of the circle. We know this because on the interval 0<q <p/2, it yields values for r on the interval 2<r<0. Since a=2 is the diameter, we can conclude that the radius is 1. Another important observation is that r=2cosq is symmetric with respect to the Polar Axis.
| q | 0 | p/6 | p/3 | p/2 | 2p/3 | 5p/6 | p | 7p/6 | 3p/2 | 11p/6 | 2p |
| r | 2 | Ö3 | 1 | 0 | -1 | -Ö3 | -2 | -Ö3 | 0 | Ö3 | 2 |
The other graph that will be discussed is our blue graph of r=2+2cos(q). This graph is a bit different. It is the graph of a cardioid which is a heart shaped figure. Again, for q in the interval 0<q<2p, we will look at a range of values for r given below. The graph of the cardioid is also symmetric with respect to the Polar Axis. Also for 0<q<p, we have values of r that range from 2<r<0.
| q | 0 | p/6 | p/3 | p/2 | 2p/3 | 5p/6 | p | 7p/6 | 3p/2 | 11p/6 | 2p |
| r | 4 | 2+Ö3 | 3 | 2 | 1 | 2-Ö3 | 0 | 2-Ö3 | 2 | 2+Ö3 | 4 |
![]()
![]()
![]()
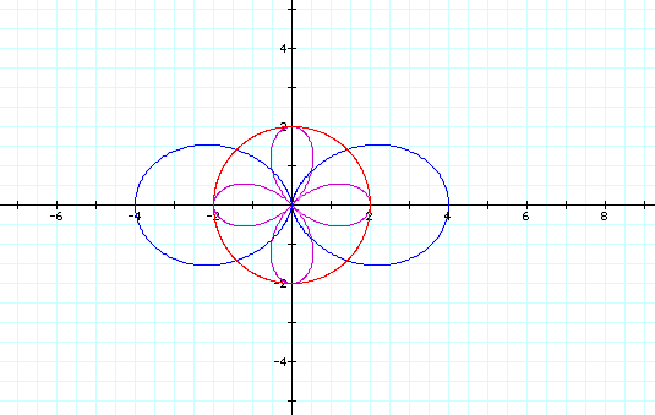
Now we can consider the n=2 case. Some interesting things happen to our graphs. Let us start with the r=2cos(2q). An observation is that we have a four pedal rose which is symmetric with respect to both the Polar Axis and the line q=p/2. The length of each pedal is 2 and two pedals are on the Polar Axis and two pedals are on the line q=p/2 line, which confirms the symmetry property. The maximum value of r is 2. Let us take a look at the table of values of r below. This table helps us to construct each pedal of our rose curve.
| q | 0 | p/6 | p/4 | p/3 | p/2 | 2p/3 | 3p/4 | 5p/6 | p | 7p/6 | 3p/2 | 11p/6 | 2p |
| r | 2 | 1 | 0 | -1 | -2 | -1 | 0 | 1 | -2 | 1 | -2 | 1 | 2 |
Now let us look at r=2+2cos(2q). In this case, we have a two pedal rose. Again, for this case the rose is symmetric with respect to the Polar Axis. Furthermore, we can also look at the range of values of r for this case as well. Notice that for 0<q<p/2, the values for r range from 4<r<0.
| q | 0 | p/6 | p/4 | p/3 | p/2 | 2p/3 | 3p/4 | 5p/6 | p | 7p/6 | 3p/2 | 11p/6 | 2p |
| r | 4 | 3 | 2 | 1 | 0 | 1 | 2 | 3 | 4 | 3 | 0 | 3 | 4 |
![]()
![]()
![]()
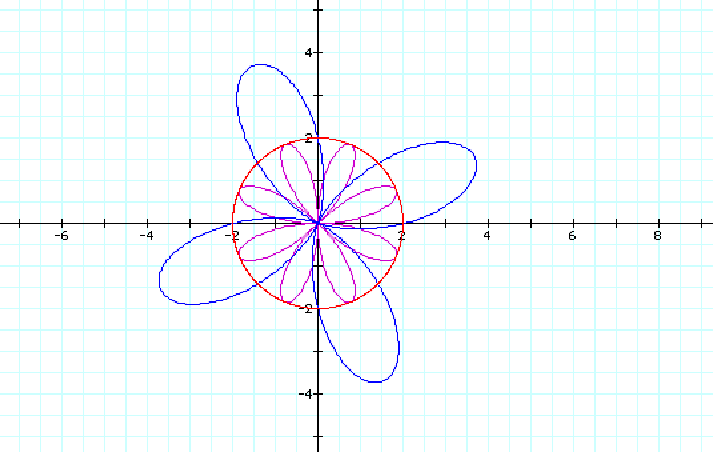
What happens as we continue to increase the values of n ? It appears that the number of pedals can be found when n is odd and when n is even. Let see if this hypothesis holds.
Consider the n=3 case. Let us discuss what happens in general for both graphs. In the case of r=2cos(3q) and r=2+2cos(3q) we only have three pedal roses. So it appears that when n is odd for both polar equations r=2cos(nq) and r=2+2cos(nq), we have n pedals. Does this conjecture hold when n is even. Let us see.
![]()
![]()
![]()
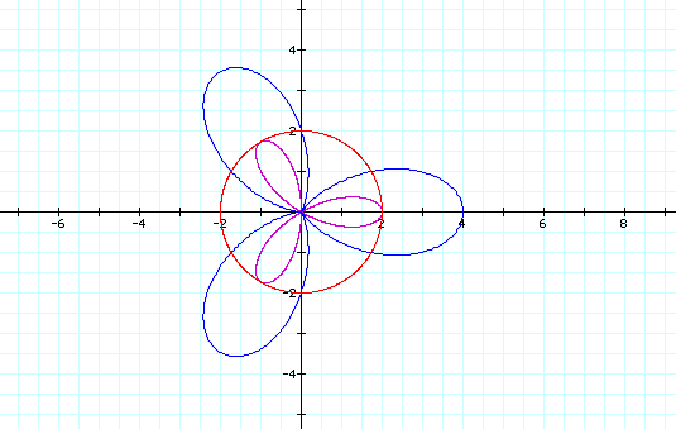
For the n=4 case, we have eight pedals for the polar equation r=2cos(4q) and only four pedals for r=2+2cos(4q). So our conclusion is a bit different than in the case of odd values of n. We can conclude that for the polar equation of the form r=2cos(nq), when n is even, we obtain 2n petals provided that n>2. But for the equation r=2+2cos(nq), we only have n petals.
![]()
![]()
![]()
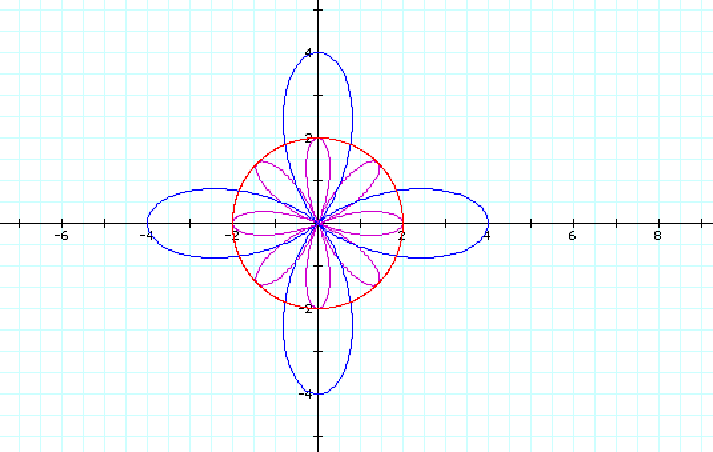
Now what if we changed our polar equations and considered the following with the same restrictions on a, b and n.
r = asin(nq) and r=a+bsin(nq)
What happens to our graph for n=0,1,2,3, and 4. Let's take a look below.
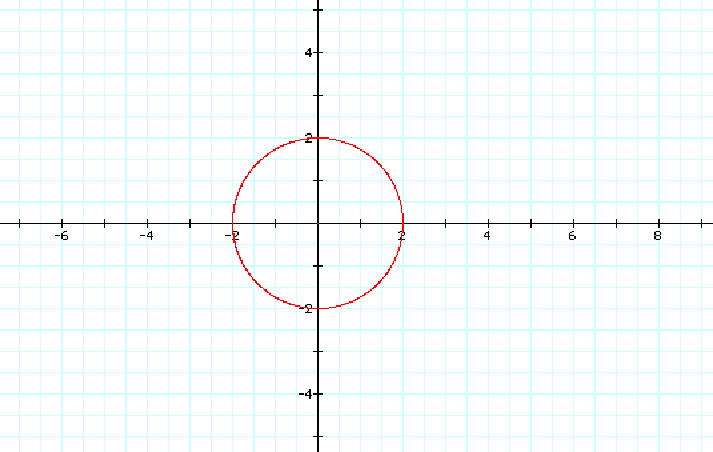
For n=0, as depicted below, the graph of three polar equations are given again including the equation of r=2. The graph of r=2sin(nq) is a point. This follows because 2sin(nq)=2sin(0)=2(0)=0. Notice also that the equations r=2+2sin(nq) and r=2 are the same. They also overlap. We have a graph of one circle such that radius is 2. This also follows because r=2+2sin(nq) simplifies to r=2+2(0) = 2.
![]()
![]()
![]()
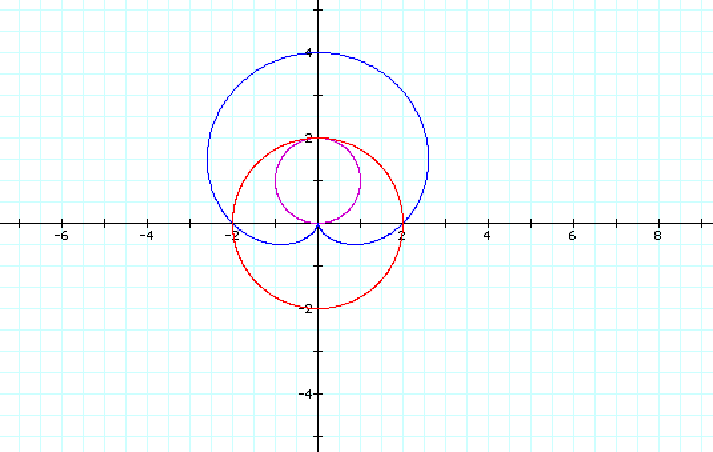
For n=1, we have the same graphs as the cosine case but they are translated by p/2. For r=2sin(q), we have a circle that is symmetric with respect to the line q=p/2. And for r=2+2sin(q) we have a cardioid that is translated the same number of radians and also symmetric with respect to the line q=p/2.
![]()
![]()
![]()
In the case when n=2, we have the rose curves again. This time in both cases, r=2sin(2q) and r=2+2sin(2q) we have symmetry with respect to the Pole. Note that the conjecture that we made for the cosine case holds here as well. That is, when n is even for r=2sin(nq) we also have 2n petals for n>2. And for r=2+2sin(nq), we have n petals as well.
![]()
![]()
![]()
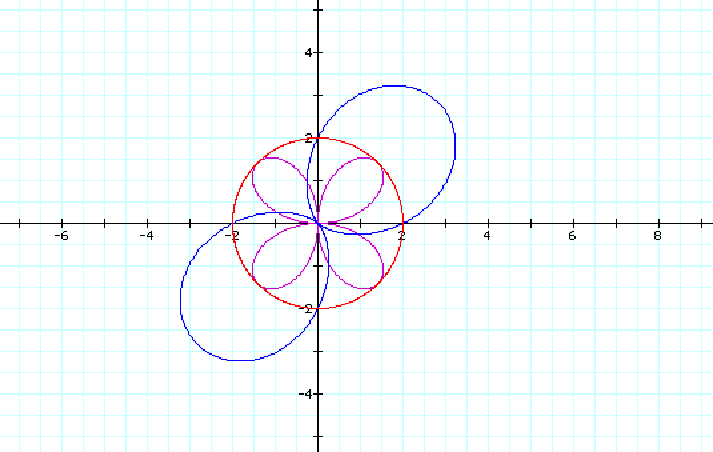
Since we have generalized, we will conclude this investigation with the cases n=3 and n=4. It looks like our conjecture holds.
When n=3,
![]()
![]()
![]()
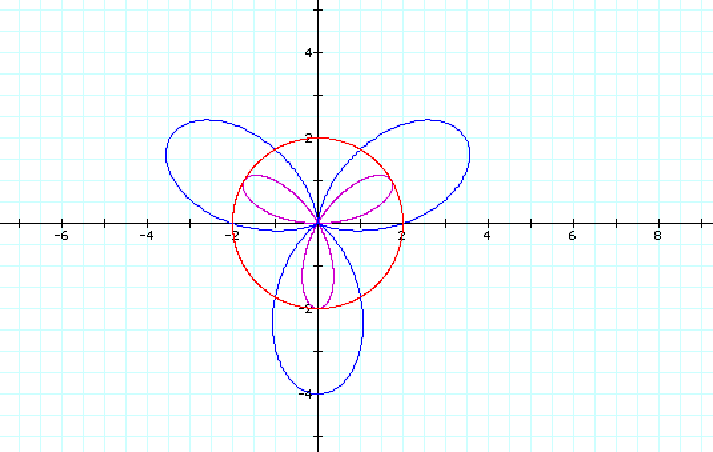
When n=4,
![]()
![]()
![]()