
Investigation of the graph y = a sin(bx+c)
By Na Young Kwon
5. Examine graphs of
y = a sin(bx + c) for
different values of a, b, and c.
Fix a and b (a=1,b=1) and
consider the graph for different values of c=-2,-1,0,1,2.
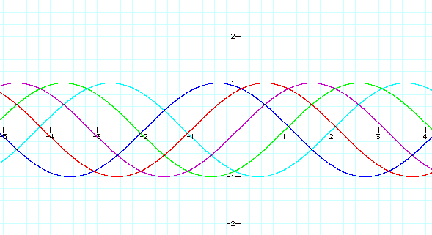
A graph of y=sin(x+c)
c=-2,-1,0,1,2 shows us similar shapes. They have the same periods
and a maximum and minimum
value. They have same cycle per regular interval.
The regular interval
is 2¹ and we call it a period. A
maximum value of these graphs is 1
and a minimum value is Ð1. The graph of y=sinx is the one that the graph of y=sin(x+1)
moves to x-axis for 1. Generally, graphs of y=sin(x+c) have a
period 2¹, the maximum
value 1 and minimum value
Ð1. If a graph of y=sin(x+c) moves to x-axis for c, it is the
graph of y=sinx.
Next, fix b and c (b=1,
c=1) and consider the graph for different values of a (a=-2,-1,0,1,2).
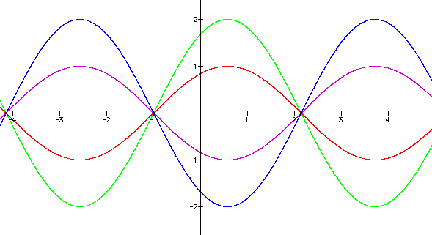
A graph of y=a sin(x+1)
(a=-2,-1,0,1,2) shows that the graphs have the same points in x-axis.
All graphs of y=a sin(x+1) meet the same points in x-axis and
the point values are
-(2¹-1), -¹-1,-1, ¹-1,
2¹-1. These graphs also have a period 2¹. The different thing is
a maximum and minimum
value. A maximum value of y=sin(x+1) and y=-sin(x+1) are
the same 1 and a maximum of
y=2sin(x+1) and y=-2sin(x+1) are the same 2. A minimum
value of y=sin(x+1) and
y=-sin(x+1) are the same Ð1 and a
minimum of y=2sin(x+1)
and y=Ð2sin(x+1) are the
same Ð2. Generally, graphs of y=a sin(x+1) have a period 2¹,
the maximum value is a and
the minimum value is Ða. If a graph of y=a sin(x+1)
moves to x-axis for 1, the
graph corresponds to y=a sinx.
Next, fix a and c(a=1,c=1)
and investigate the graph for different values of b(b=-3,-2,0,1,2).
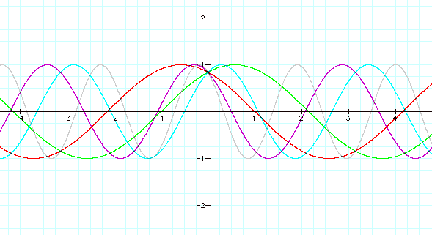
A graphs of y=sin(bx+1) have different shapes. Only graphs
of y=sin(x+1) and sin(-x+1)
have the same shapes and graphs of y=sin(2x+1) and
y=sin(-2x+1) have the same shapes.
However, all graphs have a maximum value 1 and a minimum
value Ð1.
Consider a period of graphs. Graphs of y=sin(x+1) and
y=sin(-x+1) have the same period
2¹. Graphs of y=sin(2x+1) and y=sin(-2x+1) have the same
period ¹.
Generally, graphs of y=sin(ax+1) and y=sin(-ax+1)
(a>0)have a same period 2¹/a.
All graphs of y=sin(ax+1) have a maximum value 1 and a
minimum value Ð1.
Also, if a graph of
y=sin(ax+1) (a>0) moves to x-axis for 1/a, the graph corresponds
to a graph of y=sin(ax).
Finally, letÕs investigate a graph of y=a sin(bx+c).
A graph of y=sin x has a period 2¹, a maximum
value 1 and a minimum value Ð1.
In the case of y=a sin(bx+c), the graph has a period 2¹/b, a maximum value |a| and
a minimum value -|a|. In
addition, this graph is the one that a graph of y=a sin(bx)
moves to x-axis for Ð(c/b).
ÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉ.