Polar equations
By Na Young Kwon
We will see the Polar
equations in this page.
LetÕs investigate the graph of r = a + b cos
(kq).
First, we think the case of
a=1, b=1 and k=1.
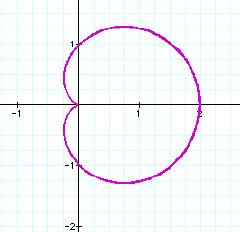
To see more graphs, we put
k=0,1,2,3 and fix a=1 and b=1.
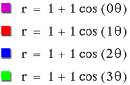
We can find as the value of k
is increasing, the number of leaf is also increasing.
When a and b are equal and k
is an integer, it is called the Ò n-leaf roseÓ.
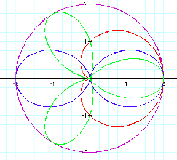
Next, we see when a=0, that
is, r = b cos(kq).
At first, fix b=1 and
investigate graphs of various k values.

Here the value of r says a
distance from original point (0,0) to some point.
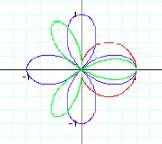
We check when r=1, the graph is
a circle, when the value of k is even,
the number of leaf is two
times of k value and when the value of k is odd,
the number of leaf is equal
to the k value.
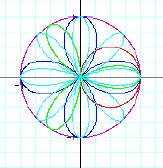
Next, we change the value of
b (b=0,1,2,3).

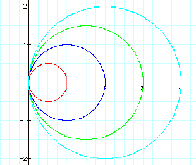
What we know here is the
value of b says a diameter of a circle.
For example, the value of b
is 2, then the graph of r = 2 cos q is a circle
which is with a diameter 2.
Next, we will see if the
value of k is changed then which graph of sin(mq)
is similar to the graph of
cos(kq).
See the following graphs.
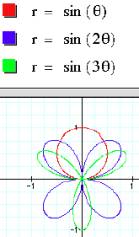
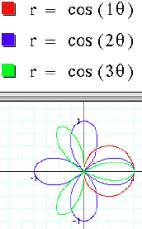
We can see the graph of sin(kq) is
similar to the graph of cos(kq).
For example, the graph of
sin(q) is rotated the graph of
cos(q) by 90 degrees.
We know that cos(q)=sin(p/2 -q). Then we change the graph expression
and see the graph.
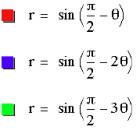
Generally, we can say the
graph of ![]() is equal to
is equal to ![]() .
.
ÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉ
Return
to Na YoungÕs Home Page