Tangent Circle
By Na Young
Given two circles A and B. Construct a circle tangent to the two circles
with one point of tangency being the designated point.

First, we make a line connecting a point A and a given point on the circle and then call the intersection point C. We construct a circle C which is the same radius with a circle B. We call the intersection point of a circle C and a line AC a point E. Next, make a midpoint of a segment BE and a perpendicular line from that point. We can construct a point D in this way. The point D is a center of circle tangent to the two circles.

The locus of a center of a tangent circle is an ellipse.
It can confirm using GSPÕs animation button.
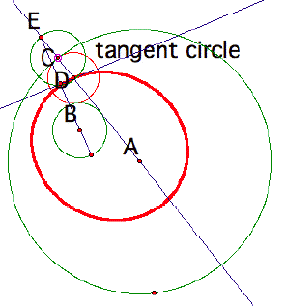
Next,
we will make a different tangent circle.
LetÕs construct the tangent circle to two given circles when the smaller circle is internal to the tangent circle.

First, we
construct a line through a center and one point of the big
circle. Call the intersection point B and make a circle of a same radius of a small circle A. Then we obtain a point C and construct a parallel line of a segment AC from a point B. The intersection point of a parallel line and a small circle is D. This is a tangent point that we want to find. Connecting D and A, we can find a center of a tangent circle O.
The locus of a center of a
tangent circle is an ellipse ,with GSP, we can animate around the big circle
and trace the locus of the center as follows:

In this investigation I found an
interesting method using GSP.
At
first, I donÕt know how to think and to use GSP. But seeing a screen of GSP and
using a pencil I draw the imaginary picture. In the picture I draw lines and
segments and through the experience, I found answers of problems.
Through
this problem solving, I knew how to use GSP and how to think using GSP. Before
solving this problem, I think GSP is just a showing mathod, however, I became
to know an important of the investigation.
ÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉ
Return
to Na
YoungÕs Home Page