Altitudes and Orthocenter
By Na Young Kwon
11. Construct any acute triangle ABC and its circumcircle.
Construct the three altitudes AD, BE, and CF. Extend each
altitude
to its
intersection with the circumcircle at corresponding points
P, Q, and R.
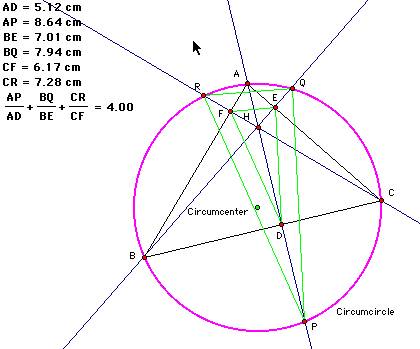
Find ![]() .___(1)
.___(1)
We can know the result is 4 by calculating GSP.
If a triangle is a regular triangle, we can easily know the result
of ![]() is 4. Because in a regular triangle the
circumcenter
is 4. Because in a regular triangle the
circumcenter
is congruent to the orthocenter and a distance from a vertex to a
circumcenter is two times of a distance from a circumcenter to
an opposite side.
What is the value of ![]() in acute triangle ABC?
in acute triangle ABC?
LetÕs prove this result.
We can find the result from the pedal triangle DEF and a triangle
PQR.
Length of
HD=Length of DP
Because a triangle
DEF is similar to a triangle PQR and the ratio is 1:2.
So we change the equation (1) the following.
![]()
![]()
We can get the following result about the area of a triangle ABC.
Area of ABC= BC * AD * 1/2 ---(1)
= AC * BE * 1/2 ----(2)
= AB * CF * 1/2 ----(3)
And area of ABC = area of HBC + area of HCA + area
of HAB
= BC*HD*1/2+AC*HE*1/2+AB*HF*1/2
Ð (4)
Because of (1)=(4), we can get
BC * AD = BC * HD+AC * HE+AB * HF
— ![]()
By (1),(2) and (3)
—
![]()
—
![]()
So we can know the
result of equation (1)
![]()
![]()
= 4
We can apply this result to the obuse triangle.
ÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉÉ
Return to Na
YoungÕs Home Page