Pedal Triangle

By Na Young Kwon

Let’s make a triangle ABC. Then if P is any plane, the triangle by constructing

perpendicular to the sides of ABC locate the three point R,S and T that are intersection.

The triangle RST is the Pedal Triangle for Pedal Point P.

Picture

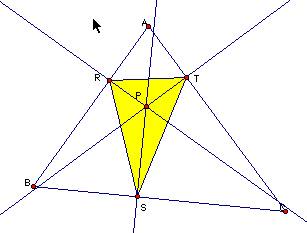
Let’s investigate if Pedal Point P is a centroid, incenter, orthocenter

and circumcenter of a triangle ABC, what is happening,

When Pedal Point P is a centroid G of a triangle ABC,

Picture

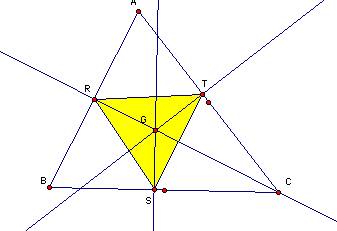
When Pedal Point P is a incenter I of a triangle ABC,

Picture

When Pedal Point P is a orthocenter of a triangle ABC,

Picture

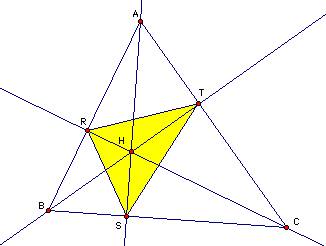
Because the orthocenter of a triangle ABC is a intersection point of perpendicular lines from a vertex to each side of ABC, feet of the perpendicular lines are three vertices of the Pedal triangle. In this case a triangle RST is called the orthic triangle or sometimes the altitude triangle.

When Pedal Point P is a circumcenter of a triangle ABC,

Picture

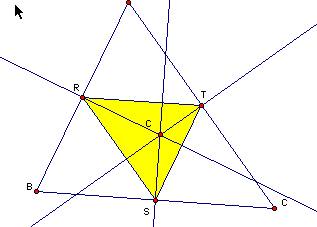
When Pedal Point is a circumcenter of ABC, a triangle RST is congruent to a medial triangle. Here we can have a question about existence of Pedal Triangle. I investigated the existence of Pedal Triangle by moving Pedal Point P. When a Pedal Point P is a vertex of triangle ABC, Pedal triangle was not made in any case. Concretely, when one of intersection points of perpendiculars to the sides of ABC is congruent to one of vertices of a triangle ABC, there is no Pedal triangle. When Pedal Point P is on a side of the triangle, Pedal Triangle exists and the line between the two perpendiculars is called the pedal line.

So I made one conjecture : Pedal triangle exists if a foot of perpendiculars of Pedal Point is not one of vertices of triangle ABC.--------(1)

In other case, we consider the Pedal point is outside of a triangle ABC. I consider the circumcircle of triangle ABC and move a Pedal point P to insideand outside of a circumcircle. First, if the Pedal point is outside of a circumcircle of ABC, then we found the Pedal Triangle exist. Second, if the Pedal point is inside of a circumcircle of ABC, then the Pedal Triangle exist. However, during these investigation I could find, when the Pedal point is on a circumcircle,

the Pedal Triangle didn’t exist. See the following pictures.

Picture 1 Picture 2

Picture 3

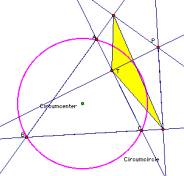
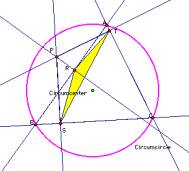
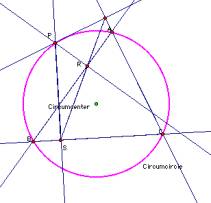
Why? How do this explain?

In picture 3 we can know feet of perpendicular lines is on the line.

In this case, we can not make a triangle. That is, The Simson line is the line containing the feet of the perpendiculars from an arbitrary point P on the circumcircle of a triangle to the sides or their extensions of the triangle.

Then my above hypothesis (1) is wrong. The sentence is corrected

: Pedal triangle exists except the following cases; if a foot of perpendiculars of Pedal Point is not one of vertices of triangle ABC; if Pedal point is on the circumcircle of an original triangle.

………………………………………………….

Return to Na Young’s Home Page