Final assignment

By Na Young Kwon

A. Consider any triangle ABC. Select a point P inside the triangle and

draw lines AP, BP, and CP extended to their intersections with the

opposite sides in points D, E, and F respectively.

Explore AF*BD*EC and FB*DC*EA for various triangles.

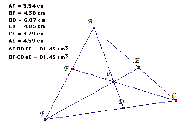
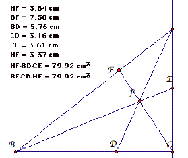
a scalene triangle a right triangle

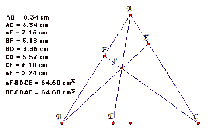
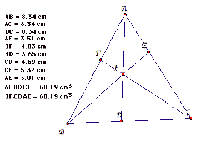
an isosceles triangle an equilateral triangle

We check the case that a point P is outside of a triangle, centroid, incenter and

circumcenter.

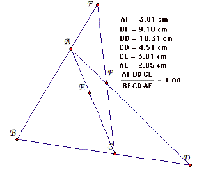
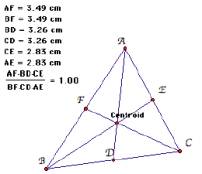
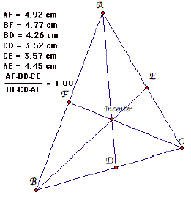
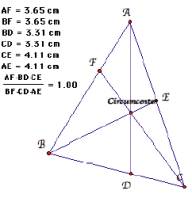
We check the value and for a right triangle, isosceles triangle and

equilateral triangle, and various location of P. Then we find an interesting

point that the value of and is equal.

B. Let’s set a conjecture with investigations.

<Conjecture>

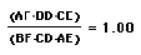
<Proof>

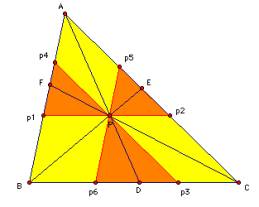
To prove it we construct the parallel lines for each side of a triangle

and call the intersection points p1,p2,p3,p4,p5 and p6 _.

See the following picture.

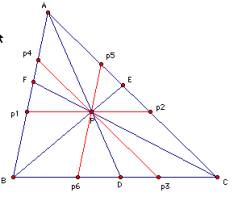
We will use the property of the parallel line and similar triangles.

At first, we change the given expression .

Multiple Pp1,Pp2,Pp3,Pp4,Pp5 and Pp6 to denominator and numerator,

and change the expression like the following:

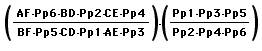----------(A)

Here, the value of is 1.

We can know this value from the following:

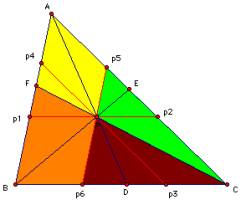
1) DCAF º DCp3 P -> CF:CP=FA:Pp3

2) DCBF º DCp6P -> CF:CP=FB: Pp6

From 1) and 2) we know FA: Pp3 =FB: Pp6 ,that is, AF× Pp6 =BF× Pp3_.

Similarly, we can know BD× Pp2 =CD× Pp1 and CE× Pp4 =AE× Pp3 _.

So, the expression (A) is changed with the following.

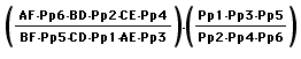
----------(B)

To find this value (B) we will also use the similar triangles.

Since DPp1p4 º D p2Pp5 , we know Pp1 : Pp2= Pp4 :p2p5 .

Thus .

Similarly, from the fact that DPp6p3 º D p5Pp2, we know .

So the value of (B) .

Hence we proved our conjecture .

From this proof, we can know the value of is 1 for an arbitrary point P .

C. Show that when P is inside triangle ABC, the ratio of the areas of

triangle ABC and triangle DEF is always greater than or

equal to 4.

When is it equal to 4?

See the following picture.

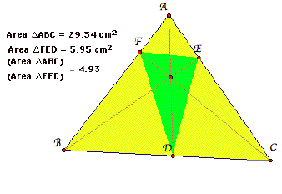
In this case we can see the result of the ratio of the areas of DABC and D DEF

is greater than 4. I found when the point P is a centroid, the ratio is equal to 4.

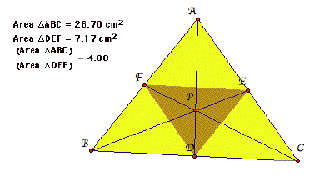
We can prove this using the definition and property of the centroid .

When point P is a centroid, BC // EF and .

So an area of triangle AEF is 1/4 of an original triangle.

An area of D FBD and D ECD is 1/4 of an area of DABC for each

because a point D is a midpoint of a segment BC. Thus an area of DDEF

is 1/4 of an area of original triangle.

………………………………………………………………

Return to Na young’s Home Page