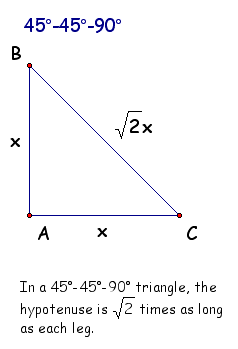
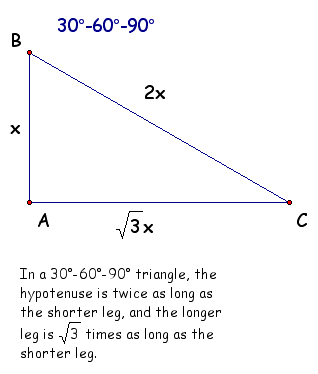
Special Right Triangles - Right triangles whose angle measures are

(1) 45-45-90 or (2) 30-60-90 are called special right triangles.

Theorems About Special Right Triangles:

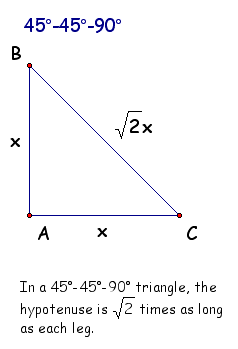
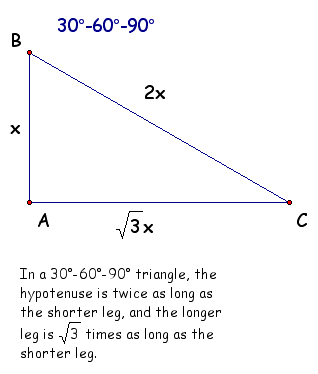
Example Problems

1. The quilt design below is based on the Wheel of Theodorus. Use the diagram to answer the following questions:

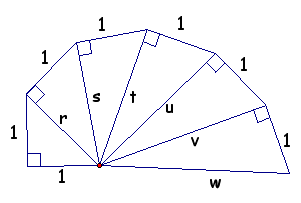
a) Find the values of r, s, t, u, v, and w. What procedure did you use?

b) Which of the triangles, if any, is a 45-45-90 triangle?

c) Which of the triangles, if any, is a 30-60-90 triangle?

Answers

a)

Do you notice a pattern from the answers above. Can you generalize a formual for n triangles in the spiral? See if you can come up with an expression for the hypotenuse for the nth triangle.

b) The first triangle is a 45-45-90 triangle because the hypotenuse is the square root of 2 and the side lengths are each

c) There is no 30-60-90 right triangle in the the diagram.

2.

a. Find the exact lengths of the legs of the triangles that are added at each stage. Leave the radicals in the denominators of fractions.

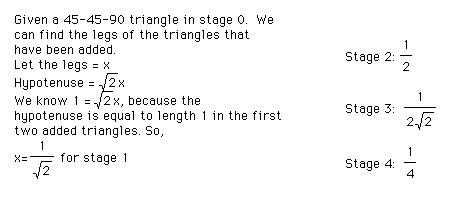
b. Describe the pattern of the lengths.

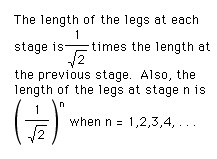
c. Find the length of a leg of a triangle added in stage 8. Explain how you found your answer.

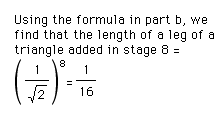
Return to Instructional Unit