

Objectives: 1. Student will learn terminology: arc length and sector area. 2. Student will use prior knowledge of circle graphs to investigate arc length and sector area. 3. Student will learn to find arc length and sector area.
Materials: Protractors, compasses, calculator, classroom computer w/ Firefly or Scan-It
Class Activity: Collect data (number of family members) from each student to develop a list of data. Tally the data. Have students generate ideas on how to convert the results of the tally into a circle graph. How do we accurately represent the results of the tally? Construct a circle graph that relates your class data. (Note: Using percentages, students determine the portion of the circle needed to represent each number from the tally. Then, they must determine how to show each percentage on the circle. They must convert each percentage to angle measurements).
At a class computer (with a Scan-It or Firefly), use a spreadsheet program to compare your circle graph to one generated by the program. How does your circle graph compare to the graph generated by the program? Are there any differences? If so, why?
Questions to Ask to generate class discussion:
How do you use relative frequency (percentage) to find the central angle measurement for each portion of the graph?
What is the sum of your central angle measurements? Why is this true?
How do the percentages relate the area of the pie wedges (sectors) to the area of the entire circle?
How do the percentages relate to the portion of the circumference (arc length) cut off by the pie wedge?
Suggested Table to chart progress of activity:
|
|
|
|
|
|
|
|
| Totals |
|
|
Questions for students to answer independently or with a partner:
1. If the radius of the circle is 1 cm, what is the area of the circle?
2. What would the area of each sector be if r = 1 cm? Fill in the appropriate column of the table. What method did you use to find each sector area? Would your method work in all cases? Write your method in a generalized format.
3. What would the circumference of the circle be if r = 1?
4. What would the length of each arc of the
circle be in this instance? Fill in the appropriate column of
the table. What method did you use to determine each arc length?
Generalize your method. How does this method compare to your method
for finding sector area?
Guided Practice:
1. Find arc length AB and the sector ACB.
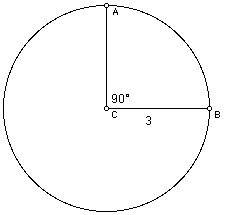
Arc Length AB:
Area of Sector ACB:
2. Find the length of arc DE and the area of sector DGE.
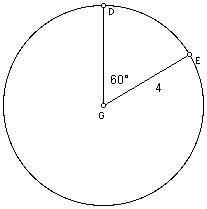
3. If the length of arc GH is 2*pi and the
circumference of the circle is 3*pi, find the central angle.
Assign homework and allow students time in class to work on assignment. Circulate throughout the room and answer student questions as the need arises.
Return to Instructional Plan Page