Have you ever been in a situation where you are trying to show the validity of something with a limited knowledge? I hope you have not. Why? Because, you just have to use your ingenuity. Let's see...

That is why I intended to write an essay on "Quadrature of Parabola" which is a famous work of Archimedes (B.C. 287-212) well known with his words "Eureka, Eureka-I have found it". The "Quadrature of Parabola" is one of his works besides crying "Eureka." This work of Archimedes has an important place in the history of mathematics since there appear the ideas of limit and integration.

Quadrature of Parabola: The quadrature of the parabola investigates the ratio between the area of the parabolic section bounded by a parabola and a chord and the area of the triangle which has the vertex of the parabolic section and two points of intersection of the segment and the parabola as its vertices (See Figure-1).

The significance of the Archimedes' solution to this problem is hidden in the fact that none of differention, integration, or coordinate geometry were known in his time. But, if you look at Greek mathematics carefully, they were using the idea of limit, or in other words "approximation".

Now let's start to Archimedes' solution to Quadrature of Parabola

Let A be the midpoint of the segment SS'. And let E and E' be the foot of the parallels from S and S' on the tangent line at V to the line passing through the points A and V. Take B as the mid-point of the segment VE and construct the segment BA' so that BA' is parallel to the segment AV. Similarly take B' as the mid-point of the segment VE' and construct the segment B'A'' so that B'A'' is parallel to the segment AV.

Construct the points C and D where the segment BA' intersect the parabola and the segment VS respectively. Similarly, Construct the points C' and D' where the segment B'A'' intersect the parabola and the segment VS' respectively.

Claim-I: The area of the triangle VCS is equal to the one-fourth of the area of the triangle VAS.

Click here to see on GSP

Proof: Since BA' is parallel to the segment VA (and so to the segment ES) and B is the midpoint of VE (i.e. VB/VE = 1/2), by Proposition-II,

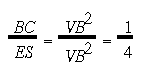(1)

Since BD = ES, BD = 4BC from (1).

If we consider Figure-3a and -3b which are extracted from Figure-2. The triangles VBD and VES are similar by A.A.A. (or A.S.A.) since BD//ES (and VE = 2 *VB). Therefore, BD/ES = VB/VE = 1/2. Since VESA is a paralleogram by construction, BA' = ES and BA'= 2BD .

On the other hand, since BC /2BD = BC/BA' = 1/4, BD = 2BC. In other words,

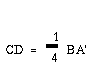(2)

Now, if we look at the triangles VCA' and SCA', we may observe that have the same altitude (since VESA is a parallelogram and B and A' are the midpoints of the sides VE and SA respectively). On the other hand, since DA'= 2CD,

Similarly,

Adding up the areas,

Since A(VAS) = 2(SA'V) and A(VCS) = A(SDC) + A(VCD), then

Then we are done.

Claim-II: The sum of the areas of the triangles VCS and VC'S' is one-fourth of the area of the triangle SVS'.

Proof: If the same argument applied to the left side of the Figure-2,

A(VAS') = 4 A(VC'S').

Therefore,

A(SVS') = 4 (A(VCS) + A(VC'S'))

Click here to see on GSP

Now, since B and B' are the mid-points of VE and VE', respectively, Proposition-III asserts that C and C' are the respective vertives of the parabolic sections VCS and VC'S'.

Consider now the two parabolic sections VCS and VC'S' with their circumscribed parallelograms (See Figure-4). Applying Claim-II each of them shows that area of the triangle VCS is four times the sum of the areas of the two blue triangles at right. Similarly, the area of the triangle VC'S' is four timesthe sum of the areas of the two blue riangles at left. Since we have seen that A(SVS') = 4 (A(VCS) + A(VC'S')), the four blue triangles together have area

Click here to see on GSP

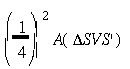
Let A = Area SVS'. Recalling that the light blue area in Figure-2 is

and that of Figure-4 is

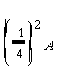
The process (forming triangles) can be repeated again and again. Thus the sum the blue triangles approximate the area of the parabolic section (See the Figure below)

A

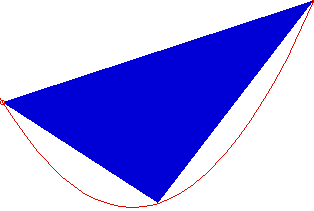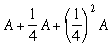In other words,

Claim-III:

Proof: Click Here for a demonstration !...

Thus,

---

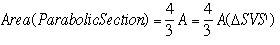
Click Here for a little example of "Quadrature of the Parabola" carried by Mapple...

mail: aerbas@coe.uga.edu

This page created February 21, 2000

This page last modified March 6, 2000