
History
The study of the circle goes back beyond the recorded history. The invention of the wheel is a fundamental discovery of properties of a circle. The Greeks considered the Egyptians as the inventors of geometry. Ahmes, who is a scribe and the author of the Rhind papyrus, gives a rule for determining the area of a circle that corresponds to 256/81 or approximately 3.16. Thales found the first theorems relating to circles around 650 BC. The Euclid's Book III, Euclid's Elements set to work properties of circles and problems of inscribing polygons. One of the problems of Greek mathematics was the problem of finding a square with the same area as given circle. Several of the 'famous curves' were first attempted to solve this problem. Anaxagoras in 450 BC is the first recorded mathematician to study this problem.
Lesson I: Definition and geometric construction of a circle
Definition
A circle, as a curve, is the set of points
equidistant from a given point. That is, a circle is a curve consisting
of all those points of a plane that lie at a fixed distance a
from a particular point, called the center of a circle,
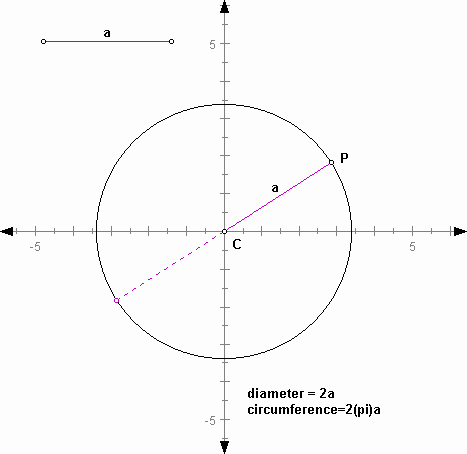
in the plane. The distance a from the center is called the radius
of the circle and the perimeter of a circle is called the circumference.
In this sense, all points on the circumference of a circle are
equidistant from its center. Diameter is the longest segment
through the center and is twice the radius, ![]() , and
circumference is given by
, and
circumference is given by ![]() .
.
If the center is at the origin of the Cartesian coordinate system:
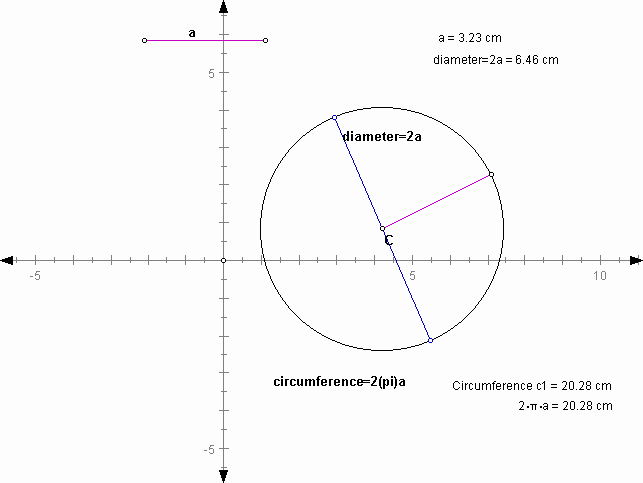
If the center is not at the origin:
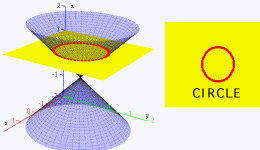
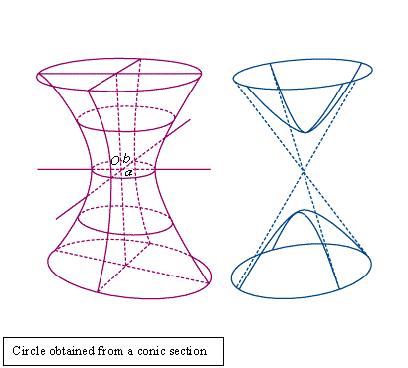
How is a circle obtained from a conic section?
A circle is obtained by the intersection of a cone with a plane perpendicular to the cone's symmetry axis. See the following figure:
Student Work: Have students construct their own circle on GSP and change the center and the radius.
Lesson II: Introduction to the algebraic representation of a circle
Equation from definition
Let's, suppose, in rectangular coordinate plane, take a point C (p, q) as a fixed point and the distance from the point (p, q) is a. Since r is the distance, we don't need to specify that a is a positive number. We are looking for the equation of the circle, which is satisfied with such conditions given. If you want to find a point P (x, y) on the circle, it can be traced in the Cartesian plane. Now you have:
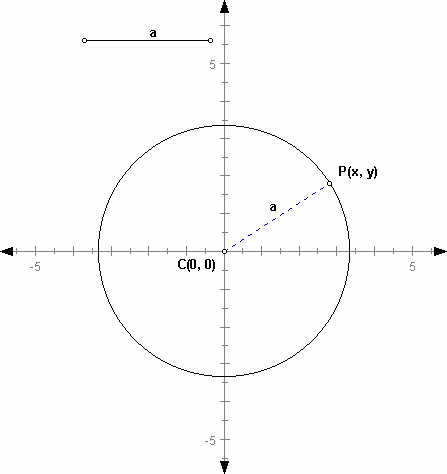
1) If the center lies on the origin of the plane:
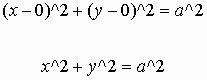
2) If the center is not concurrent with the origin:
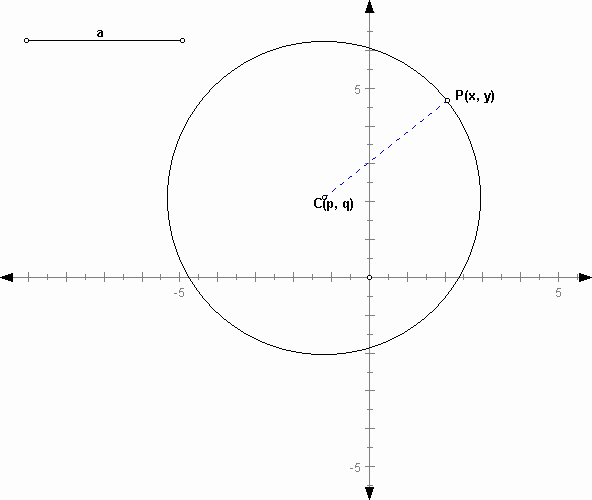
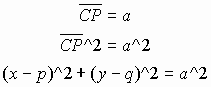
The above formula is considered as the standard equation of a circle. The fixed point C (p, q) is the center and r is the radius of this circle, according to the definition. Given any equation of this form, you can guess the geometric figure corresponding to this equation is a circle with the center (p, q) and radius r. If you have the origin (0, 0) as the center, that is you put 0 into a and b, you get the equation
Prerequisite: In order to draw the final equation form mathematically from the word sentence, you should first know the definition of distance as a mathematical term and express it with mathematical sentence like the first equation. You also have to understand the Pythagorean theorem to get the distance between any two points.
Lesson III: Analytic Equation of a Circle
Let's suppose the center of a circle is not at the origin (0, 0) (See Figure 5.). We already have the equation and can expand:
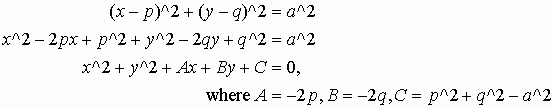
The last formula is called a general quadratic equation of a circle. In fact, this formula is a general equation for all conic section curves. If you change the value of A, B, and C, you may get a circle, a parabola, an ellipse, or a hyperbola. On the contrary, given the general quadratic equation, if C is positive, the equation represent a circle having the center (p, q) and radius expressed in terms of a square root.
Lesson IV: Parametric and Polar Equations of a Circle
We can get a circle in polar coordinates. When the center is at the origin (0, 0), in figure 4, according to definition of a circle, you have:
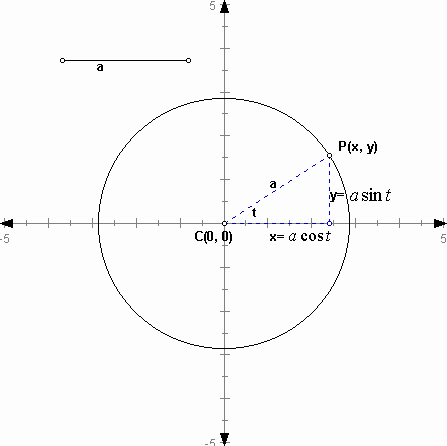
The parametric equations for a circle of radius r are:
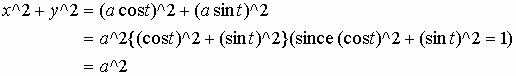 .
.The polar equation for a circle having the center at (0, 0) and the radius a is:
For a circle having the center at (p, 0) and the radius a, the polar equation is:
Similarly, the polar equation for a circle with the center at (0, q) and the radius a is:
Lesson V: Properties of a circle
The ratio of circumference to diameter is always constant, denoted by p , for a circle with the radius a as the size of the circle is changed. Let's define d as diameter and c as circumference. Then, as observed, since
the ratio is:
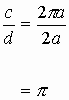
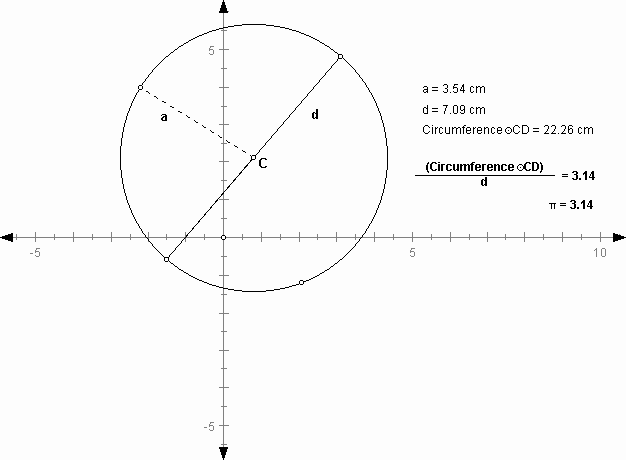
Exploration: Apollonius Circles
Definition: The locus of a point P whose distances from two fixed points A and A' are in a constant ratio 1 : m , so that
Investigate the Apollonius Circles.
References
Coxter, H. S. M. (1969). Introduction to Geometry. New York: John Wiley & Son, Inc.
http://mathworld.wolfram.com/Circle.html