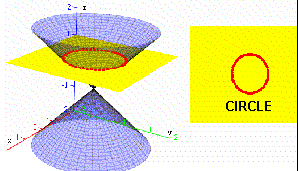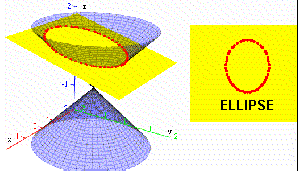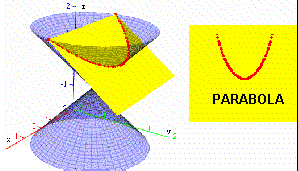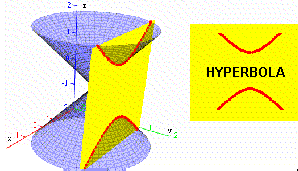

A conic (or conic section) is a plane curve
that can be obtained by intersecting a cone with a plane that
does not go
through the vertex of the cone. There are three possibilities,
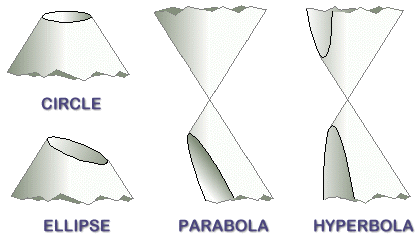
depending on the relative position of the cone and the plane (Figure
1).
If no line of the cone is parallel to the plane, the intersection is a closed curve, called an ellipse.
If one line of the cone is parallel to the plane, the intersection is an open curve whose two ends are asymptotically parallel; this is called a parabola.
Finally, there may be two lines in the cone parallel to the plane; the curve in this case has two open pieces, and is called a hyperbola.
Conic sections are among the oldest curves, and is an old mathematics topic studied systematically and thoroughly. The conics seem to have been discovered by Menaechmus (a Greek, c.375-325 BC), tutor to Alexander the Great. They were conceived in an attempt to solve the three famous problems of trisecting the angle, duplicating the cube, and squaring the circle. The conics were first defined as the intersection of: a right circular cone of varying vertex angle; a plane perpendicular to an element of the cone. (An element of a cone is any line that makes up the cone) Depending on whether the angle is less than, equal to, or greater than 90 degrees, we get ellipse, parabola, or hyperbola respectively. Appollonius (c. 262-190 BC) (known as The Great Geometer) consolidated and extended previous results of conics into a monograph Conic Sections, consisting of eight books with 487 propositions. Quote from Morris Kline: "As an achievement it [Appollonius' Conic Sections] is so monumental that it practically closed the subject to later thinkers, at least from the purely geometrical standpoint." Book VIII of Conic Sections is lost to us. Appollonius' Conic Sections and Euclid's Elements may represent the quintessence of Greek mathematics.
Appollonius was the first to base the theory of all three conics on sections of one circular cone, right or oblique. He is also the one to give the name ellipse, parabola, and hyperbola.
In Renaissance, Kepler's law of planetary motion, Descarte and Fermat's coordinate geometry, and the beginning of projective geometry started by Desargues, La Hire, Pascal pushed conics to a high level. Many later mathematicians have also made contribution to conics, especially in the development of projective geometry where conics are as fundamental objects as circles are in Greek geometry. Among the contributors, we may find Newton, Dandelin, Gergonne, Poncelet, Brianchon, Dupin, Chasles, and Steiner. Conic sections is a rich classic topic that has spurred many developments in the history of mathematics.
(from http://xahlee.org/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html)
History
Lesson I: Definition and geometric construction of a circle
Lesson II:
Lesson III:
Lesson IV:
Lesson V:
Lesson VI:
In-class Worksheet:
Exploration:
PARABOLA
(by A. Kursat ERBAS)
Lesson I: Definition and geometric construction of a parabola
Lesson II: Introduction to the algebraic representation of a parabola
Lesson III: Analytic Equation of a Parabola
Lesson
IV: Understanding the simplest
parabolas of the form ![]()
Lesson V: Polar and Parametric Equations of a Parabola
Lesson VII: Reflective (Optical) Property of Parabola
Lesson VIII: Properties of tangents to a parabola
Lesson IX: Area property of a parabola
ELLIPSE (by A. Kursat ERBAS)
Lesson I: Definition and Basic Properties of Ellipse
Lesson II: Introduction to the algebraic representation of an ellipse
Lesson III: Polar and Parametric Equations of an Ellipse
Lesson IV: Circumference and Area of an Ellipse
Lesson V: Reflective (Optical) Property of an Ellipse
History
Lesson I: Introduction
Lesson II:
Lesson III:
Lesson IV:
Lesson V:
In-Class Worksheet:
Lesson VI:
References:
http://xahlee.org/SpecialPlaneCurves_dir/ConicSections_dir/conicSections.html
http://www.astro.virginia.edu/%7Eeww6n/math/ConicSection.html
http://www-groups.dcs.st-andrews.ac.uk/%7Ehistory/Curves/
