
Lesson I: Definition and Basic Properties of Ellipse
Definition: Ellipse is commonly defined as the locus of points P such that the sum of the distances from P to two fixed points F1, F2 (called foci) are constant. That is, distance[P,F1] + distance[P,F2] = 2 a, where a is a positive constant.
|
|
|
 |
|
Student Work:
At this point allow students to draw their own sketches on the
computers and observe some properties of the ellipse.
Before students spend several minutes on observing and playing with the ellipse, introduce two important lines (axes) for an ellipse, major and minor axes, and the vertexes of an ellipse (See Figure 2).
Vertexes
of the ellipse are defined as the intersections of the ellipse
and a line passing through foci. The distance
between the vertexes are called major axis or focal
axis. A line passing the center and perpendicular to the major
axis is the minor axis.
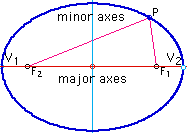 |
![]() Click here to investigate parabolas
on an interactive java applet (If you do not have GSP software
on your computer, it's an perfect opportunity to take a look at.)
Click here to investigate parabolas
on an interactive java applet (If you do not have GSP software
on your computer, it's an perfect opportunity to take a look at.)
![]() Click
here
for an interactive java applet game which is about to find
the foci of an ellipse.
Click
here
for an interactive java applet game which is about to find
the foci of an ellipse.
![]() Click
here for an interactive java applet
toy to construct ellipses with a tool called "Ellipsograph".
Click
here for an interactive java applet
toy to construct ellipses with a tool called "Ellipsograph".
![]() Click
here for a java applet to investigate
relative properties of two congruent ellipses.
Click
here for a java applet to investigate
relative properties of two congruent ellipses.
Lesson II: Introduction to the algebraic representation of an ellipse
Analytic Equation of an Ellipse
Before introducing a general equation (i.e. the analytic, polar or parametric form) of an ellipse, it is important to understand where this equation comes from. Thus, before giving a formal equation of an ellipse, deal with the following construction of the equation with referring to the notation on the Figure 3:
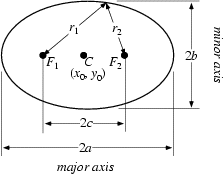
First of all notice that
![]()
(Why? Let the students think about the picture below!)
Let an ellipse lie along the x-Axis and find the equation of the Figure 3 where F1 and F2 are at (-c,0) and (c,0). In Cartesian Coordinates,
![]()
![]()
![]()
![]()
![]()
Since
![]()
This makes the equation in the simplest form:
![]()
If, instead of being centered at (0, 0),
the Center of the ellipse is at ![]() ,
equation becomes
,
equation becomes
![]()
In class explorations:

Lesson III: Polar and Parametric Equations of an Ellipse
As can be seen from the Cartesian Equation for the ellipse, the curve can also be given by a simple parametric form analogous to that of a circle, but with the x and y coordinates having different scalings,
In Polar Coordinates, the Angle![]() measured
from the center of the ellipse is called the Eccentric Angle.
Writing
measured
from the center of the ellipse is called the Eccentric Angle.
Writing![]() for the distance of a point from
the ellipse center, the equation in Polar Coordinates is just
given by the usual
for the distance of a point from
the ellipse center, the equation in Polar Coordinates is just
given by the usual
Here, the coordinates ![]() and
and
![]() are written with primes to distinguish
them from the more common polar coordinates for an ellipse which
are centered on a focus. Plugging the polar equations into the
Cartesian equation (9) and solving for
are written with primes to distinguish
them from the more common polar coordinates for an ellipse which
are centered on a focus. Plugging the polar equations into the
Cartesian equation (9) and solving for ![]() gives
gives
Lesson IV: Circumference and Area of an Ellipse
Circumference: The circumference of an ellipse with major axis radius, a, and minor axis radius, b, is given (approximately) by
Area: The area of an ellipse with major axis radius, a, and minor axis radius, b, is given by
The Area of an arbitrary ellipse given by the Quadratic Equation
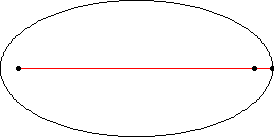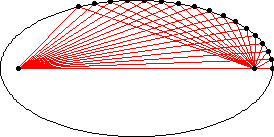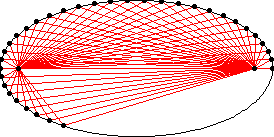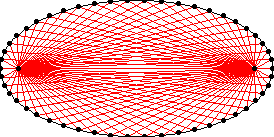
Lesson V: Reflective (Optical) Property of an Ellipse
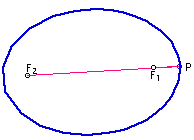
In an ellipse, lightrays from one focus will reflect to the ther focus (See Figure 4).
|
|
![]() Click
here for an interactive java applet
to investigate reflection (optical) property of an ellipse.
Click
here for an interactive java applet
to investigate reflection (optical) property of an ellipse.
Students' Investigations
Investigation 1. The locus of points for a fixed point on the coming ray (from F2 to P) is an ellipse (See Figure 5). Why? What kind of evidences do we have? What properties does it have (like where is its foci--hint: one of them is F2)?
|
|
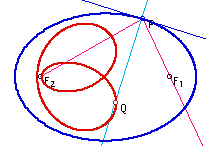
Investigation 2. What is the locus of points for a fixed point Q on the reflected ray (from P to F1) is an ellipse? (See Figure 6 for various locus which depends on the location of Q). Describe the properties of this curve?
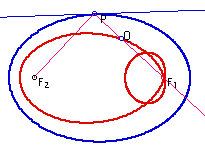 |
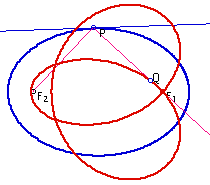 |
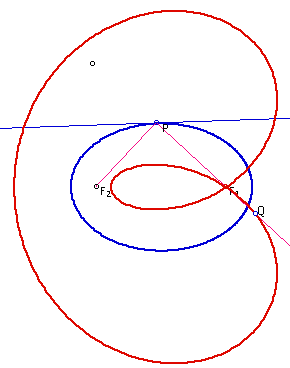 |
|
|
|
|
Investigation 3. What happens if Q is on the normal line at the point Q (See Figure 7).
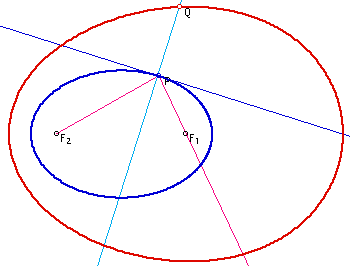 |
 |
|
|
|
