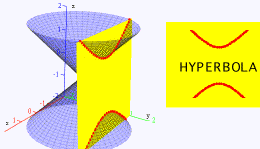

History
In Renaissance, Kepler's law of planetary motion, Descarte and Fermat's coordinate geometry, and the beginning of projective geometry started by Desargues, La Hire, Pascal pushed conics to a high level. Many later mathematicians have also made contribution to conics, especially in the development of projective geometry where conics are fundamental objects as circles in Greek geometry. Among the contributors, we may find Newton, Dandelin, Gergonne, Poncelet, Brianchon, Dupin, Chasles, and Steiner. Conic sections is a rich classic topic that has spurred many developments in the history of mathematics.
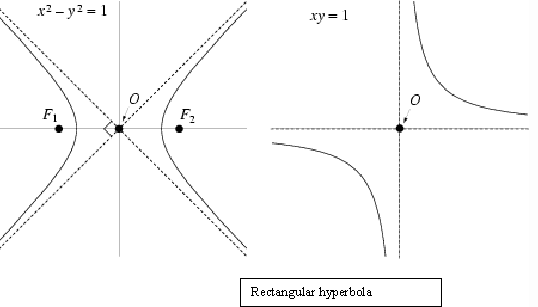
Menaechmus first studied a special case of the hyperbola. This special case was xy = ab where the asymptotes are at right angles and this particular form of the hyperbola is called a rectangle hyperbola.
Euclid and Arisaeus wrote about the general hyperbola but only studied one branch of it while Apollonius who was the first to study the two branches of the hyperbola gave the hyperbola. The focus and directrix of a hyperbola were considered by Pappus.
Exploration about Mathematician: Apollonius
Lesson I: Introduction

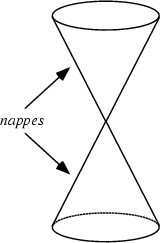
Hyperbola describes a family of curves. Together with ellipse and parabola, they make up the conic sections. Hyperbola is two-branched open curve produced by the intersection of a circular cone and a plane that cuts both nappes (see Figure 2.) of a cone. of a cone. [A cone is a pyramid with a circular cross section ] A degenerate hyperbola (two intersecting lines) is formed by the intersection of a circular cone and a plane that cuts both nappes of the cone through the apex.
Lesson II: Definition and geometric construction of a hyperbola
Hyperbola is defined as the locus of points P (x, y) such that the difference of the distance from P to two fixed points F1(-c, 0) and F2(c, 0) that is called foci are constant. The midpoint of the two foci points F1 and F2 is called the center of a hyperbola.
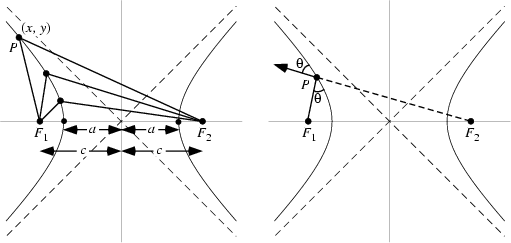
That the x-intercept of locus P (x, y) is at (-a, 0) and (a, 0) gives
So the constant ![]() is
is ![]() , that
is twice the distance between the x-intercepts.
, that
is twice the distance between the x-intercepts.
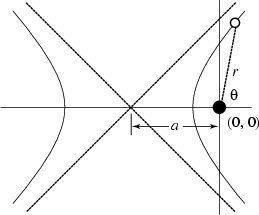
Another definition is that as the path (locus) of a point moving so that the ratio of the distance from a fixed point F (the focus) to the distance from a fixed vertical line (the directrix) is a constant, greater than one. (The hyperbola, however, because of its symmetry, has two foci.)
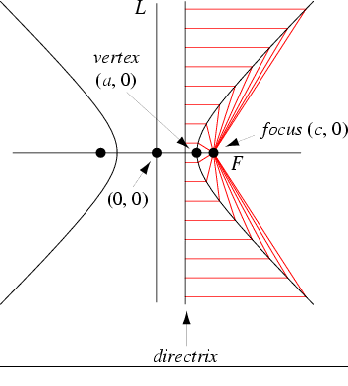
If we let d be the distance from the center on which the directrix lies and R ratio, then we have
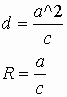
Lesson III: Analytic equation of a hyperbola
From the first definition we can draw the equation of a hyperbola (See the Figure 3):
Since
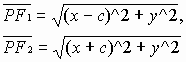 ,
,Squaring both sides, we get
Again, divide both sides of this equation by
then we obtain
Since
substitute ![]() with
with ![]() ,
,
we have
which is called the standard equation of a hyperbola.
Lesson IV: Properties of a hyperbola
Eccentricity e can be, in verbal, explained as the fraction of the distance to the semimajor axis at which the focus lies, where c is the distance from the center of the conic section to the focus. Let the distance between foci be 2c, then e (always bigger than 1) is defined as
The eccentricity e describes the "flatness" of the hyperbola.
Asymtotes of a hyperbola is defined as a curve approaching a given curve arbitrarily closely.
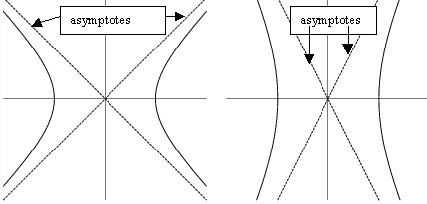
You can get the equation of asymptotes from the standard equation of a hyperbola
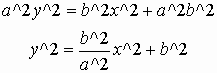
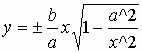
In the final equations, ![]() goes
to 0 if
goes
to 0 if ![]() goes to infinite. According to this, the hyperbola
becomes close to one of the equations,
goes to infinite. According to this, the hyperbola
becomes close to one of the equations,
We called these equations
as the asymptotes. As a result, the asymptotes can be written as
Lesson V: Rectangular Hyperbola
When the asymptotes of a hyperbola are perpendicular, the hyperbola is called rectangular. This occurs when the semimajor and semiminor axes are equal. This also means that
Further, it gives
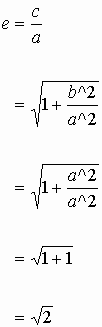
Lesson VI: Parametric and polar equations of a hyperbola
The parametric equations of a hyperbola are:
The polar equation of a hyperbola with the center at a focus is:
Lesson VII: In-class Worksheet
References
http://mathworld.wolfram.com/Hyperbola.html
http://xahlee.org/SpecialPlaneCurves_dir/Hyperbola_dir/hyperbola.html