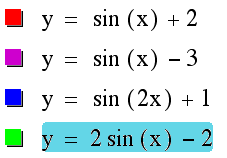This assignment involved examining the graphs of y=a sin (bx+c) for different values of a, b, and c. This examination was done by exploring the different components separately and then observing the interaction. The changes caused by altering the values of a were explored first. The next component was the effects of b. After a final examination of various values for c, the interaction of these three variables was explored.
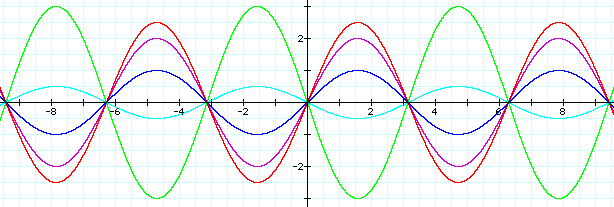
The first item explored in this study was the variable a. Variable a was the variable which affected the amplitude of the sin wave. As a increased, the amplitude of the wave increased. As a decreased, the amplitude decreased. When a was given a negative value, the graph flipped upside down. The picture below illustrates the waves produced by different values of a. These changes in amplitude are directly proportional to the changes in a. When a is given the value 2, the amplitude is 2 times greater than the amplitude of the wave when a = 1. When a = 1, the amplitude is equal to 1. When a = -3, the amplitude is equal to 3. This means that the absolute value of a is equal to the amplitude of the wave.
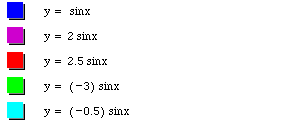
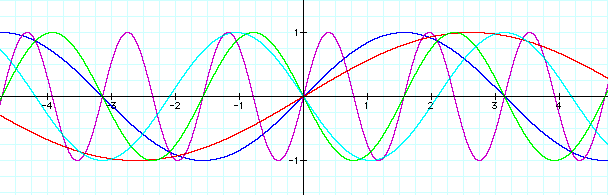
The second item explored was the variable b. This variable affected the wavelength of each sin wave. As b increases, the wavelengths decreases, but as b decreases, the wavelength increases. The wavelength (which is also known as the period) of a wave is inversely proportional to the value of b. In the example below, when b = 1, the wavelength is equal to 2pi. When b = 4, the wavelength is equal to pi/2. The same inverse relationship occurs when b is given a negative value. When b = -2, the wavelength is equal to pi. The wavelength of a sin wave with the equation y = a sin (bx+c) is determined by the formula wavelength = (2)(pi)/(b).
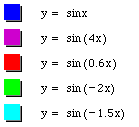
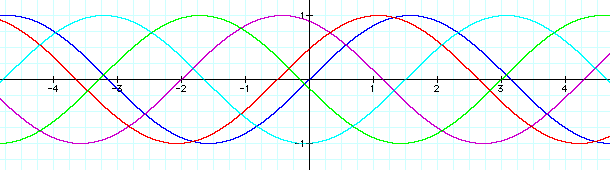
The final variable in the equation was the variable c. The horizontal displacement is represented by c. When c is equal to 2, the graph of the sin wave is shifted to the left 2 units. When c is equal to -1.5, the graph is shifted to the right 1.5 units. The sign of c, therefore, determines the direction to which the graph is shifted. If c is negative, the graph is shifted to the right. If c is positive, the graph is shifted to the left. The absolute value of c determines the magnitude of total displacement.
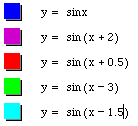
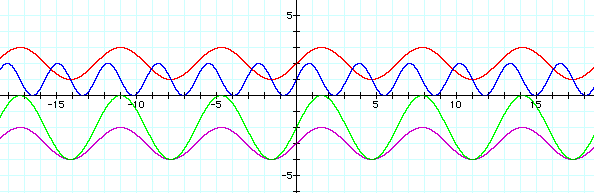
An extension of this exploration involves the introduction of a third variable, the d variable. This variable is written into the equation as y = a sin (bx+c) + d. The d variable affects vertical displacement. As shown below, when d = 2, the sin wave is shifted up two units. When d = -3, the sin wave is shifted down three units. The d variable, therefore, determines the magnitude and direction of the vertical shift on asin wave graph. The magnitude of the shift is equal to the absolute value of d, while the direction of the shift depends on the sign of d. (If the sign is negative, the graph is shifted down. If the sign is positive, the graph is shifted up.)