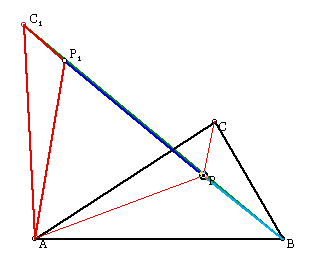
---

Proof that the Fermat Point minimizes the distance AP + BP + CP

---

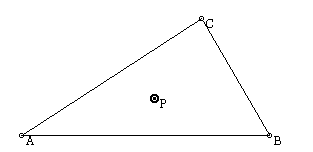
Given triangle ABC, we can choose an arbitrary point P in the interior of the triangle, as shown below.

Next, we construct the triangle APC. If we rotate it 60 degrees to the left, we have the triangle AP1C1. Note that this makes APP1 an equilateral triangle, so the distance P1P is equal to the distance AP. WE also know, by construaction, that the distance C1P1 is equal to the distance CP. It is obvious that the distance BP is equal to the distance BP, so BP + PP1 + C1P1 = BP + AP + CP.

To minimize this distance, we need to create P so that the distance BC1 is minimal.

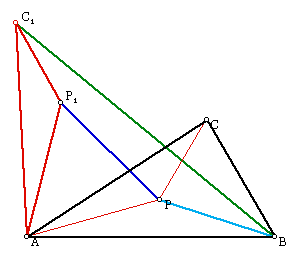
To minimize the distance BC1, we need to use what we know about distance. The shortest distance between two points is a straight line. Therefore we need to place P on the line BC1 so that P1 is also on the line BC1. This is identical to connecting the vertices of the equilateral triangles on the sides of ABC to their opposite vertices. This concludes the proof of the Fermat Point.